Algoritmos Evolutivos

"Evolution is cleverer than you are" FRANCIS CRICK

Computación evolutiva

Son metaheurísticas que emulan la evolución biológica, aplicando un mecanismo análogo a los procesos evolutivos naturales para resolver problemas de búsqueda y optimización. Utilizan selección natural, reproducción (recombinación y mutación) y diversidad genética para seguir la idea de la supervivencia de los individuos más altos, la cual se evalúa de acuerdo al problema a resolver con una función de fitness.

Esquema de un algoritmo evolutivo sobre una población \(P\):

Inicializar(P(0));
generación = 0;
mientras (no Criterio Parada) hacer
Evaluar(P(generación));
Padres = Seleccionar(P(generación));
Hijos = Aplicar Operadores Evolutivos(Padres);
Nueva Población = Remplazar(Hijos(generación));
generación++;
P(generación) = Nueva Población;
fin
retornar Mejor Solución Encontrada

Definición y Conceptos

Un AE trabaja sobre una población de individuos que representan soluciones potenciales al problema a resolver. La representación de un individuo se le llama genotipo y la solución fenotipo.

Un AE selecciona mediante la función de fitness. La evolución consiste en 4 pasos:

1. Evaluación: Calcular fitness de cada individuo
2. Selección: Determinar candidatos adecuados para la nueva generación
3. Aplicar Operadores evolutivos: Genera descendientes a partir de los individuos seleccionados.
4. Reemplazo: Mecanismo para el reemplazo generacional.

La población se inicializa de forma aleatoria o siguiendo heurísticas específicas. Existen diversas políticas de selección y reemplazo que definen a un algoritmo:

1. Elitismo (privilegiar a los mejores)
2. Aumentar la presión selectiva
3. Aumentar la diversidad genética
4. etc.

Los operadores evolutivos determinan el mecanismo de exploración del espacio de soluciones. Los más populares son los de recombinación y mutación. Finalmente, el criterio de parada define como concluye el AE: Nro. generaciones, delta del fitness, estimaciones de error, etc.

Paradigmas

Existen 3 paradigmas fundamentales en la teoría de la computación evolutiva:

1. Algoritmos Genéticos (Genetic Algorithms)
2. Programación Genética (Genetic Programming): Evolución de programas (estructuras con contenido semántico)
3. Estrategias de Evolución (Evolution Strategies) Evoluciona variables (números reales) del problema y de la propia técnica.

Programación Genética

John Koza (1996) propuso el mecanismo evolutivo de programación genética para generar programas, extendiendo ideas previas de Cramer sobre representaciones con árboles de parsing

Propone un mecanismo evolutivo para crear (síntesis o inducción) programas de alto nivel. Utiliza un set de terminales para representar variables independientes a las cuales se le aplican variables primitivas. Por ejemplo, andar cambiando los operadores y variables de un programa LISP ( - ( - x 1 ) (* x ( * x x ) ) )

Algoritmo:

1. Generar una población inicial a partir de la composición de funciones y terminales en forma aleatoria o heurísticas
2. Aplicar Iterativamente los pasos a) y b) a la población de programas hasta que se cumpla un criterio de parada
    a) Ejecutar cada programa de la población y asignarle su valor de fitness
    b) Crear una nueva población de programas a partir de aplicar las cuatro operaciones, sobre programas seleccionados con una probabilidad relacionada su fitness
3. Retornar el mejor programa encontrado

Estrategias de Evolución

Fue propuesta para la optimización de parámetros con números reales en problemas complejos. Originalmente modelaba los propios valores a optimizas, generando un único descendiente a partir de un padre (Modelo 1+1). Se basaba en el operador de mutación Para la generación de un nuevo individuo se utiliza una formula aritmética: \[ x^{t+1} = x^t + N(0,\sigma) \[ Donde \(N\) es la distribución Gaussian (media y desviación estándar).

Esta propuesta se extiende luego al modelo \((\mu + \lambda)\) (Selección entre padres e hijos) y \((\mu,\lambda)\) (Selección entre hijos únicamente).

Regla del éxito 1/5: establece que la razón entre mutaciones exitosas y el total de mutaciones debe ser 1/5. En caso de ser mayor, se debe incrementar la desviación estándar; en caso contrario, se debe decrementar

Para el modelo \((\mu,\lambda\) es 1/7. La estrategia clave de estos algoritmos es la autoadaptación: Mecanismo mediante el cual además de evolucionar las variables del problema, también se evolucionan los parámetros de la técnica. Se suele utilizar como parámetro de ajuste la desviación estándar.

Algoritmos Genéticos

Enfatizan la importancia de del operador de recombinación sobre el de la mutación. La recombinación opera como operador principal, mientras que la mutación es un operador secundario. Tienen fitness y usan selección probabilista. El clásico algoritmo usa representación de cadena binaria

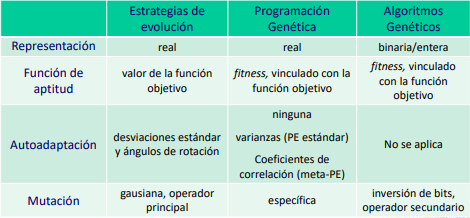
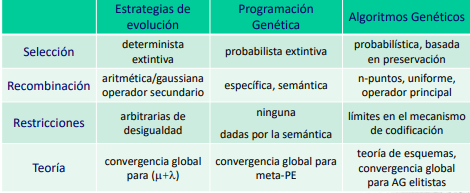
Comparación

Los AG trabajan a nivel del genotipo (codificación) mientras que los GP y ES a nivel de fenotipo. AG y GP usan selección probabilista, mientras que ES es determinista El operador principal en AG es la recombinación y el secundario mutación y no suelen ser adaptativos. En GP la recombinación está limitada por la semántica. Y ES se basa en mutación con autoadaptación de parámetros.

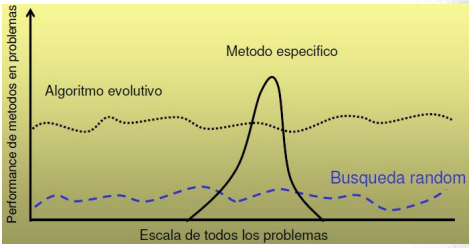
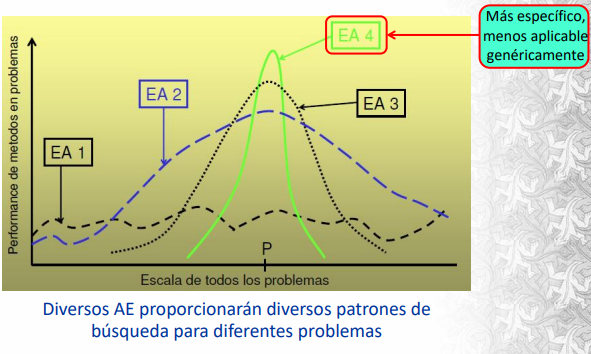
Si bien no hay una opinión unánime sobre las ventajas, es calara su versatilidad para la resolución de problemas en áreas muy variadas. Esto es porque son altamente útiles para resolver problemas con espacio de soluciones de dimensión elevada o no muy bien comprendido. Al igual que en problemas multimodales donde podemos quedar atrapados en óptimos locales.

Es importante destacar que la búsqueda del mecanismo evolutivo es independiente de las particularidades del dominio, lo que permite definir esquemas genéricos capaces de abordar múltiples problemas. No son sensibles a la función a optimizar en el sentido de que les afecte la no-linealidad, diferenciabilidad, convexidad, etc. A su vez no necesita conocimientos específicos del problema, aunque se puede incorporar conocimiento para mejorar la búsqueda.

Ventajas

• Simplicidad conceptual del mecanismo de exploración
• Amplia aplicabilidad
• Superiores a métodos tradicionales en muchos problemas reales
• Pueden incorporar conocimiento sobre el dominio del problema
• Pueden hibridizarse con otras técnicas de búsqueda
• Son robustas a los cambios dinámicos
• En general, pueden auto adaptar sus parámetros
• Explotan de modo natural las ventajas del procesamiento paralelo

Desventajas

• Han sido duramente criticadas por los investigadores de la IA simbólica por considerarlas, en forma equivocada, inferiores a las búsquedas aleatorias
• La programación automática fue considerada una “moda pasajera” y el enfoque evolutivo fue visto como otro intento por lograr lo imposible
• Los especialistas de IA clásica las consideran “mal fundamentadas” e “inestables”
• Su alta aplicabilidad las hace poco eficientes para algunos tipos específicos de problemas (No Free Lunch Theorem)
• Sin incorporar conocimiento del problema, pueden tener problema para hallar los óptimos globales
• Su eficiencia computacional puede ser pobre, demandando grandes recursos de cómputo para problemas complejos

No Free Lunch Theorem

Teorema de optimización demostrado por Wolpert y Macready en 1995. Establece que todos los algoritmos que buscan optimizar (hallar min o max) una función se comportan de la misma forma al ser promediados sobre todas las posibles funciones a optimizar.

El teorema justifica por qué ante el conjunto de todos los problemas de optimización matemáticamente posibles, en promedio, los algoritmos se comportarán exactamente de la misma manera. Puede ser visto como una justificación para incorporar la mayor cantidad de conocimiento posible al dominio de un problema.

“A general-purpose universal optimization strategy is theoretically impossible, and the only way one strategy can outperform another is if it is specialized to the specific problem under consideration" (Ho and Pepyne, “Simple Explanation of the No-Free-Lunch Theorem and Its Implications”, 2002)

En el powerpoint se detecta un COPE. Diciendo que no responde a si es más eficiente para el subconjunto de problemas "del mundo real" que son de interés resolver. Lmao. ¿Por qué no admitir que es un mecanismo muy potente cuando se combina con conocimientos específicos de un problema? ¿Por qué tratan de exponer los AG como una panacea a los problemas de búsqueda?

Algoritmos Genéticos

Conceptos biológicos.

1. Cromosoma: Cada una de las cadenas de ADN que se encuentran en el núcleo celular.
2. Locus: lugar que ocupa un gen en un cromosoma en particular
3. Alelo: Valores que pueden tomar un gen
4. Gametos: células que transportan la información genética para efectuar la reproducción sexual.
5. Las células haploides tienen un solo cromosoma, las diploides dos.
6. Se denomina genotipo a la información contenida en el genoma
7. Los rasgos específicos y observables de un individuo constituyen su fenotipo.
8. La aptitud de un individuo es la capacidad de adaptarse a su entorno
9. La selección es el proceso donde algunos individuos son seleccionados para reproducirse. Se le dice dura cuando se escoge a los mejores individuos, y blanda cuando se usan mecanismos probabilistas.
10. La reproducción consiste en la creación de un nuevo individuo a partir de dos progenitores (reproducción sexual) o de un único progenitor (reproducción asexual). Aquí ocurre la recombinación o cruzamiento.

Características

Se denomina explotación al proceso de utilizar la información obtenida de puntos del espacio de búsqueda previamente visitados para determinar los puntos que conviene visitar a continuación. Esto involucra movimientos finos.

Se denomina exploración al proceso de visitar nuevas regiones del espacio de búsqueda para tratar de encontrar soluciones prometedoras. Implica grandes saltos en el espacio de búsqueda.

Técnicas de búsqueda estocástica, utilizan selección probabilista y trabajan sobre una representación de las soluciones. A cada posición de la cadena se le denomina gen. A la cadena general se le llama cromosoma, a cada subcadena en la cadena general se le denomina gen y al valor dentro de cada posición se le llama alelo. En codificación binaria solo hay dos valores posibles: 0 o 1.

El proceso de selección tiene que buscar un compromiso entre búsqueda del espacio de soluciones y explotación de buenas soluciones. En el algoritmo genético simple (Ags) se utiliza la técnica de rueda de ruleta. Otras opciones son selección por rango, torneo, etc.

La decodificación debe aplicarse antes de evaluar las soluciones, ya que la función de fitness opera sobre los fenotipos.

Un AG tiene cinco componentes básicos:

1. Una representación de las soluciones potenciales del problema.
2. Un procedimiento para crear una población inicial de posibles soluciones (ej proceso aleatorio)
3. Una función de evaluación que representa al "ambiente" clasificando las soluciones en términos de su aptitud.
4. Un conjunto de operadores de evolución que alteran la composición de los individuos de la población a través de las generaciones
5. Una configuración paramétrica (tamaño de la población, probabilidad de cruzamiento, probabilidad de mutación, criterio de parada, etc.)

En general los AG trabajan sobre una población de tamaño fijo. El tamaño de la población debe ser un número tal que permita mantener diversidad en los individuos solución, sin sacrificar la eficiencia computacional del mecanismo de búsqueda. Las probabilidades de aplicación de los operadores evolutivos definen el balance entre la exploración del espacio de búsqueda y la explotación de buenas soluciones.

Usualmente se determinan los valores apropiados mediante análisis empíricos y procedimientos estadísticos.

Representación

La representación es el genotipo que se corresponde con una solución al problema. Por ello, existe un proceso de codificación y decodificación.

Soluciones no factibles

Son las soluciones del algoritmo que no son una solución real al problema (no cumplen la forma o restricciones). Para lidiar con este frecuente problema existen 4 estrategias:

• se descarta la solución. (se pierde diversidad)
• se trata de corregir la solución.
• se penaliza la solución en el fitness. Para problemas puede ser dificultoso requiriendo estudios teóricos para definir un modelo de penalización.

Algoritmo Genético Simple (AGS)

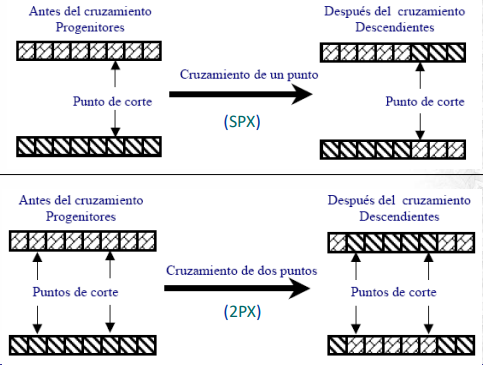
Propuesto por Goldberg, es el clásico: Rep binaria, selección por rueda de ruleta, cruzamiento de un punto y mutación bit flip.

Fases de un algoritmo genético:

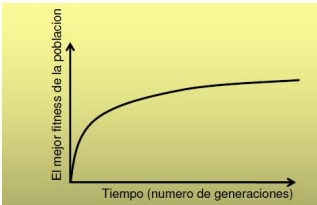
Se puede observar como el fitness escala de forma logarítmica. Lo que indica que vale la pena las ejecuciones largas dependiendo de la importancia que se les asigne a los últimos progresos. Por otro lado, puede verse que no vale la pena hacer buen esfuerzo en la inicialización de buenas soluciones. Sin embargo, es un enfoque útil si se conoce buenos métodos de inicialización para el problema.

Conocimiento del dominio

Modelos de Evolución

En los AE tradicionales el paso evolutivo básico involucra la generación de la nueva población de individuos. Por ello se les denomina modelo generacional. Existen variantes como el de estadio estacionario steady-state y el de un único individuo.

Estado estacionario

Cada paso de la evolución consiste en la selección de dos padres para efectuar un cruzamiento, produciendo uno o dos descendientes. Los individuos creados pueden mutar y luego se colocan en la población reemplazando a alguno ya existente.

Es una interesante combinación entre los mecanismos de exploración (ya que mantiene las características poblacionales) y explotación (ya que hace un movimiento hill-climbing presionando a los individuos mejor adaptados). Suelen usarse técnicas de selección elitistas.

Un problema de este es que requiere 2P selecciones para cada P miembros de la población creados. Por lo que el genetic drift es mayor que el de un algoritmo generacional.

Modelo de gap generacional

Este es un modelo intermedio el cual tiene como característica que se determina un porcentaje de la población que participará en la reproducción. A su vez puede ser de tipo solapado \((\mu, \lambda)\) o no solapado \((\mu + \lambda)\) .

Existen luego otras variantes como los Messy GA y los algoritmos evolutivos paralelos. Hay todo un ruido con este modelo del gap generacional, donde diversos estudios muestran problemas con el gap alto y tamaño de la población. Ver las presentaciones para más información.

Estrategias elitistas

El elitismo es requerido como condición teórica para hallar el óptimo global de un problema de optimización (De Jong, 1993)

En general en un modelo de estado estacionario el elitismo está implícito en la política de reemplazo. Se dice que el mecanismo evolutivo converge cuando los individuos de la población son muy parecidos entre sí. Para evitar convergencia prematura se tratan de usar técnicas para mantener la diversidad poblacional.

Notas del practico

Vamos a diseñar nuestros algoritmos evolutivos utilizando jMetal. jMetal.

Repaso preliminar

¿Cuándo son útiles los AE? Los AE nos sirven para resolver problemas complejos y/o escenarios grandes, problemas que admitan soluciones sub-óptimas, diseño de soluciones que no siguen ideas intuitivas.

En otras palabras, si el problema es simple, necesitamos la soluciono optima o sabemos que las soluciones tienen un diseño evidente -> Los algoritmos evolutivos no son la herramienta más adecuada al problema.

Que debemos definir para usar AE:

1. Representación de soluciones.

2. Función de evaluación.

3. Método de initialization.

4. Operadores evolutivos.

5. Criterio de selección.

6. Criterio de reemplazo.

7. Condición de parada.

8. Configuración de parámetros.

Representación

Toda solución candidata al problema debe poder ser representada. Se deben evitar representar soluciones no factibles. Ya que malgasta esfuerzo computacional, complejiza el proceso de codificación/decodificación.

La representación va a implicar dos funciones de codificación y decodificación para poder construir las soluciones, su complejidad depende de las características del problema.

Las codificaciones binarias más populares son: Número binario, códigos de Gray, FloatingPoint IEEE. Existen otras particulares al problema planteado. Ver: Grafos.

Función de evaluación

¡Debe estar claramente formulada! Debe asignar un valor de fitness a cada una de las soluciones factibles, debe estar implementada de forma eficiente ya que esta se utiliza constantemente. Suele afectar fuertemente el desempeño computacional del AE.

Criterios de una buena función de fitness:

• La función de fitness depende del problema y del criterio de optimización
• Opera directamente sobre las soluciones del problema (fenotipos)
• Debe considerar las restricciones del problema
• Puede definir objetivos múltiples (función vectorial, problemas multi-objetivo) o incorporar sub-objetivos
• Puede cambiar dinámicamente a medida que un AE procede en la exploración (problemas dinámicos)
• La función de fitness es una caja negra para un AE Input: fenotipo Output: valor de fitness

La función de fitness puede ser muy costosa de evaluar algorítmicamente, puede ser multivalued, e inclusive puede tener una expresión analítica desconocida (por ejemplo, debe estimarse con simulaciones)

Uno de los mecanismos más usados en la función de fitness para mejorar su eficacia es el escalado. Permite solucionar la dominancia prematura de individuos muy adaptados y la caminata aleatoria (randow walk). Básicamente se escala la función de fitness utilizando métodos lineales, truncamiento sigma o escalada potencia. Ej:

1. escalado lineal: \(F' = a \times F + b\) .
2. Sigma: \( F' = F - (F - c * \sigma) \) donde sigma es la variación de fitness de la población.
3. Escalado potencia: \( F = F^k \)

Initialization

Siempre debe involucrar un proceso aleatorio para otorgar diversidad a la población inicial. aunque se puede incorporar conocimiento del problema sesgando la población con soluciones semilla. También se pueden utilizar otros algoritmos para generar soluciones iniciales.

Operadores evolutivos

Debemos definir operadores de recombinación y mutaciones que se adapten a la codificación utilizada. ¿Decidir qué acción tomar ante soluciones invalidas? (Descarto, penalizo o corrijo). Como manejo las soluciones invalidas (Luego de aplicar cada uno de los operadores (overhead+) o al terminar de aplicar todos los operadores). Considerar aplicar hibridaciones con otras técnicas.

En cada generación se aplican los operadores evolutivos

1. Se seleccionan padres de acuerdo a su valor de fitness
2. Se cruzan los padres para producir descendientes
3. Se mutan aleatoriamente los nuevos descendientes
4. Se insertan los nuevos individuos creados, que reemplazan a algunos de la generación anterior

Otros

El criterio de selección: Aplicar una adecuada presión selectiva equilibrando explotación y exploración. Una presión de selección alta puede generar convergencia prematura. Mientras que una presión de selección baja puede conducir a una búsqueda muy lenta e ineficaz.

El mecanismo de muestreo es el que determina la selección de los cromosomas. La precisión y eficacia de un algoritmo de muestreo puede evaluarse según el Sesgo (pye), amplitud (set de valores que puede tomar el número real de descendientes) y complejidad computacional. Existen diversas técnicas las cuales se agrupan en estocásticas, deterministas y mixtas. Las estocásticas están la famosa rueda de ruleta y el muestreo estocástico universal (que preserva la diversidad) Las deterministas está la selección truncada, la de bloque, elitista, reemplazo generacional y reemplazo elitista. Las mixtas incluyen selección por torneo (grupos random) y selección por torneo estocástico (probabilidad random de ganar).

Deriva genética (genetic drift):

- Fuerza evolutiva que actúa junto con la selección natural, cambiando las frecuencias alélicas de las especies en el tiempo Normalmente se da una pérdida de los alelos menos frecuentes y una fijación (frecuencia próxima al 100%) de los más frecuentes, resultando una disminución en la diversidad genética de la población

El criterio de reemplazo: Hay dos modelos más utilizados (Los hijos generados reemplazan a los padres -> Padres e hijos compiten para pasar a la siguiente generación).

El criterio de parada puede ser por un esfuerzo prefijado (#generaciones,#evaluaciones,execution time) o por detección de convergencia

Configuración paramétrica implica definir los parámetros del mecanismo de evolución del problema. Por ejemplo, pC (probabilidad de combinación),pM (probabilidad de mutación) y #Población.

Implementación de AE with jMetal.

jMetal proviene de Java METaheuristic ALgorithms. Es una lib orientada a objetos para abordar problemas de optimización con metaheurísticas (incluyendo AE) y soporte para problemas multiobjetivo.

Para el informe se espera que citemos a los autores que se encuentran en la ppt, en cuanto al uso de jMetal

Se precisa Java11 JDK, Maven para el manejo de dependencias y un entorno de desarrollo.

SubProyectos jMetal

1. jMetal-core : Clases principales de jMetal (interfaces, abstracts, operadores, codificación, etc.)
2. jMetal-algorithm: Algoritmos disponibles (GA (generacional y de estado estacionario), NSGA-II,etc.)
3. jMetal-problem: Problemas de ejemplo y benchmarks. (ej: OneMax, StringMatching, etc.)
4. jMetal-example: Ejemplos de resolución de problemas. (Están las soluciones de los problemas en jMetal-problem)
5. jMetal-lab: Permite el diseño de estudios para comparar metaheurísticas
6. jMetal-experimental: Funcionalidades experimentales. (Inestable)
7. jMetal-parallel: Funcionalidades para paralelar algoritmos.

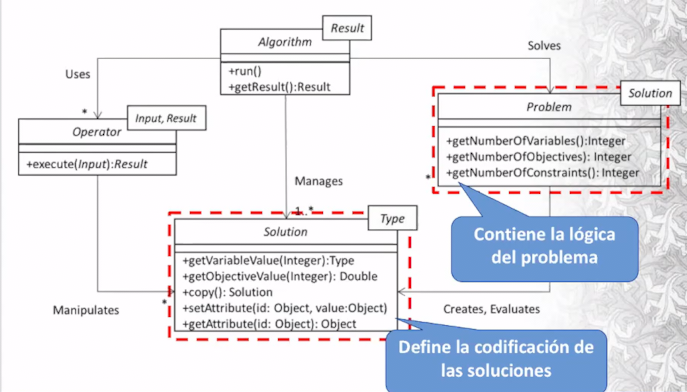
Uso jMetal

Problem debe implementar dos métodos: evaluate que evalúa el genotipo de una solución y createSolution que tiene la capacidad de crear una solución. El objeto Problem es el indicado para contener la información de la instancia del problema a resolver.

Ya existen algunos modelos de problemas como Binary Problem. Recordar que hay una sola instancia de la clase problema por solución.

Ahora con el problema ya definido, debemos aplicar algún algoritmo para su resolución. En el curso nos vamos a centrar en algoritmo mono-objetivo Genetic Algorithm. Por lo general los algoritmos están pensados para resolver problemas de minimización.

Técnicas Avanzadas

Se presentan técnicas avanzadas para los algoritmos evolutivos.

Codificación diploide.

Un genotipo en una codificación diploide consta de dos cromosomas (en AGS se tiene un cromosoma por codificación). Esto crea redundancia en la formación cromosómica, y es necesario un criterio de desambiguación.

Un criterio puede ser el de dominancia. Esto es, para cada gen, cuál va a ser el gen dominante y cual el recesivo. Los genes dominantes son los que se van a expresar en la solución. Las características dominantes se expresan en hemo cigotos (AA->A) y heterocigotos (Aa->A) Las características recesivas solamente se expresan en homocigotos (aa->a)

¿Por que esto es necesario? Es un mecanismo para preservar la diversidad, es un mecanismo de memoria para recordar valores que no resultan útiles en la actualidad

Particularmente útil en entornos dinámicos, donde la definición de lo que es útil cambia con el ambiente y el tiempo.

Aplicación en AE

Una propuesta pionera por Hollstein es el modelo evolutivo de dos loci. Se tiene un gen funcional: 0,1 y gen modificador m,M. Los alelos de valor 0 son dominantes cuando hay por lo menos una M presente en el gen modificador.

Otra alternativa es el modelo trialelico. Es una simplificación de dos loci. Extiende el alfabeto de valor \(\Sigma\) utilizando un único locus. Cada tabla es para cada gen.

Que alelo es el dominante puede ser estático o dinámica. Se determina cual va a ser el alelo dominante3 y cual el recesivo. El modelo diploide mantiene un adecuado nivel de diversidad reduciendo la necesidad de mutación y evitando las caminatas aleatorias de esta.

Esta es una técnica que introduce memoria al algoritmo evolutivo. Permite almacenar características que han sido buenas en el pasado y tal vez sean buenas en el futuro en entornos dinámicos.

Inversión y reordenamiento

La inversión es un mecanismo utilizado para reducir el sesgo de los operadores de cruzamiento de n puntos respecto al largo de definición de los esquemas. La idea des reordenar las posiciones potencialmente relacionades. Observar que el gen sigue siendo el mismo, simplemente estamos cambiando el orden de en qué se despliega. Es decir, se modifica el genotipo, pero el fenotipo permanece sin cambios. Esto ya complica el cruzamiento de soluciones en forma directa.

¿De que sirve este operador? La idea es juntar los genes que están fuertemente relacionados entre sí. Esto nos sirve para cuando se hace un operador de cruzamiento los genes relacionados no sean partidos a la mitad, ya que estaríamos perturbando excesivamente la solución. Como consecuencia, vamos a estar generando mejores hijos.

Representación de permutaciones

Es utilizada en problemas de optimización combinatoria donde se busca una permutación que optimice una cierta función objetivo. Por ejemplo, en el problema TSP donde cada entero es el id de un nodo, tenemos el problema que los operadores tradicionales no pueden ser aplicados trivialmente (¡no podemos repetir ids!.), es necesario usar operadores específicos.

operadores para la representación de permutaciones

Un operador para el crossover es el PMX (Partially Mapped Crossover). Actúa intercambiando secciones entre dos puntos de corte (como 2px - two point crossover), pero corrige en base al mapping entre padres.

Primero se intercambian las secciones del crossover. Luego se corrigen estas utilizando el mapping de que nodos fueron modificando. Recorriendo el genotipo para obtener el individuo que está repetido. La guía a este operador de cruzamiento para permutaciones está orientada a mantener las posiciones absolutas de los elementos codificados en los individuos.

Otro operador es el OX (Order Crossover). Es similar al PMX, pero no corrige por intercambios, sino que genera huecos que se desplazan en orden circular a partir del segundo punto de corte. Los huecos se mapean con el otro individuo.

A diferencia de PMX donde se mantenían las posiciones absolutas, en OX se mantienen las posiciones relativas de los individuos.

Finalmente tenemos el CX (Cycle Crossover). Se seleccione un valor en un individuo y se completa con los mapping correspondientes en el otro individuo, hasta obtener un ciclo. Posteriormente se completa con los valores "sobrantes" del otro individuo. Este operador de cruzamiento mantiene los ciclos.

Mecanismo para aumentar la diversidad

A continuación, se listan los siguientes mecanismos de preservación de la diversidad:

• Diferenciación sexual
• Especialización y nichos
• Técnicas de crowding (crowding y crowding determinista)
• Fitness sharing
• Restricciones al cruzamiento

Su objetivo es preservar la mayor cantidad de características de los individuos presentes en la población.

Diferenciación Sexual

En la naturaleza no todos se pueden reproducir con todos... Tenemos ciertos tipos de soluciones que solamente se pueden reproducir con otras. Esto crea una cierta estructura característica en la población que permite que se crean dos espacios de soluciones particulares.

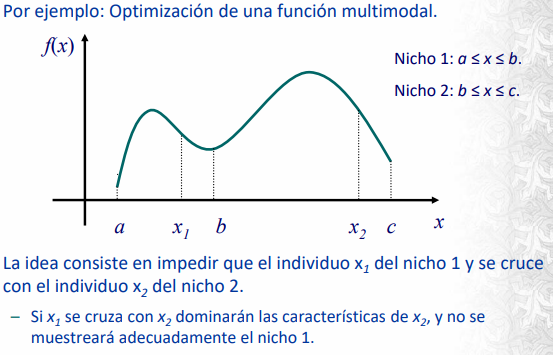
Especialización y nichos

Es un mecanismo basado en la definición de categorías. Los individuos se separan en clases y realizan un rol especifico en el organismo. Es muy utilizado en problemas multimodales o de fitness variable. Se aplican restricciones al cruzamiento en subpoblaciones y castas.

Técnicas de crowding

Se quiere evitar tener todas las soluciones crowdeadas en un lugar :). ¿Cuando voy a reemplazar, a cuáles voy a sustituir? En vez de incorporar restricción explicita en el cruzamiento, cada nuevo individuo reemplazara al individuo más similar a si mismo existente en la población.

Hay un parámetro llamado Crowding factor que determina la cantidad de individuos contra los que se compara cada nuevo individuo.

Existe una variante llamada crowding determinista donde cada descendiente compite en torneo con sus padres. Sustituyendo al padre más cercano de acuerdo a una función de distancia.

Determinar la función de distancia es uno de los desafíos que trae esta técnica.

Fitness Sharing

La idea consiste en decrementar el fitness de las zonas muy representadas del espacio de búsqueda. Se determina un grado de vecindad entre individuos sumando para cada uno de ellos los valores de una función S (función de Sharing) correspondientes con cada vecino. Se trabaja con valores de fitness reducido f_r

\[ f_r (x_i) = \frac{f(x_i)}{\sum_j SH(d(x_i,x_j))} \]

Restricciones de cruzamiento

La idea es prevenir o minimizar la aparición de individuos poco aptos. Para lograrlo se introduce un sesgo en la recombinación de individuos tratando de incrementar la eficiencia del algoritmo. Hay tres propuestas:

1. Castas con cruces ocasionales: Tenemos las soluciones en castas, las cuales se reproducen internamente mientras el fitness observado mejore, cuando deja de haber mejora se permite el cruzamiento entre castas.

2. Mating templates: Los individuos tienen su valor funcional y un patrón para el apareamiento. La idea es que cada individuo tiene una función que le indica si puede aparearse con otra solución o no.

3. Restricción basada en distancia: El cruzamiento solo está autorizado entre individuos cuyas características difieran como mínimo en un valor dado. El objetivo de esto es logara un cruzamiento efectivo que potencia la exploración del espacio de soluciones.

Fundamentos Teóricos

Por qué funcionan los algoritmos evolutivos?

Existen dos enfoques seguidos para analizar los fundamentos de los algoritmos evolutivos

1. Teoría de los esquemas (schema theorem): Esquema clásico de Holland y Goldberg. Se caracteriza por contabilizar el mecanismo de muestreo.
2. Ver el algoritmo evolutivo como un proceso estocástico Markoviano.

Schema Theory (Goldberg)

Un esquema es un formato o patrón que especifica una propiedad de un conjunto de soluciones, por lo cual caracteriza parcialmente a una solución en el espacio de genotipos. Se extiende el alfabeto de soluciones \(\Sigma\) para incluir el \(*\) el cual representa cualquier carácter de \(\Sigma\) . De esta forma se tienen \((k+1)^l \) esquemas para un alfabeto de tamaño \(k\) y tiras de largo \(l\). Una población de tamaño n va a contener entre \(2^l\) y \(n2^l\) schemas.

¿Cual es la utilidad de los esquemas?

Los individuos en forma aislada no son útiles para el análisis, ya que compiten con otros individuos. Es necesario considerar las clases de individuos (esquemas), que permiten describir en forma precisa las similitudes entre los individuos de una población y estudiar su influencia sobre el proceso de búsqueda

Se definen las siguientes funciones: \( o(H) \) como la cantidad de posiciones definidas en un esquema \(H\) . Largo de definición de un esquema H: \(\delta(H)\) es la distancia en posiciones entre el primer y último valor definido de H. \(E1=0111*\) tiene \(o(E1)\) = 4 y \(\delta(E1) = 5 – 1 = 4 \) . Sea \(m(H,t)\) el número de individuos representantes del esquema H en la generación t.

La idea detrás del análisis consiste en identificar similitudes entre los individuos de la población y relacionarlas con los valores altos de la función de fitness. Se considera el efecto que tienen los operadores evolutivos sobre la evolución de los schemas

Sea \(f\) la función de fitness y \(\bar{f}\) el fitness promedio de la población, se puede modelar el efecto de la selección de un esquema como:

\[ m(H,t+1) = m(H,t).\frac{f(H)}{\bar{f}} \]

Suponiendo que el fitness promedio de la población es constante. Puede llegarse a la siguiente formula (Donde c es una constante tal que \(f(H) = \bar{f}+c.\bar{f}\) ) :

\[ m(H,t+1)=(1+c)^t . m(H,0) \]

Entonces, el operador de selección opera asignando exponencialmente copias de los individuos mejor adaptados y extinguiendo las características de los menos adaptados.

Por otro lado, el operador de cruzamiento es destructivo y estocástico. Por lo que debe trabajarse con la probabilidad de que un esquema sobreviva al operador. Lo cual para SPX es:

\[ P_s(H) \geq 1- \frac{\delta(H)}{l-1} \]

Donde \(P_s\) es la probabilidad de supervivencia y \(l\) el largo de la tira.

En cuanto a la mutación bitflip debe considerarse la posibilidad de supervivencia de un esquema como

\[ P_s(H) = (1- p_M)^{O(H)} \approx 1-o(H).p_M\]

Donde \(p_M\) es la probabilidad de mutación. Suponiendo que esta probabilidad es muy pequeña puede aplicarse taylor para llegar a la segunda igualdad. Juntando todas las ecuaciones se puede llegar al teorema de los esquemas:

\[ m(H,t+1) \geq m(H,t). \frac{f(H)}{\bar{f}} . (1 - (p_c.\frac{\delta(H)}{l-1}) - o(H).p_M ) \]

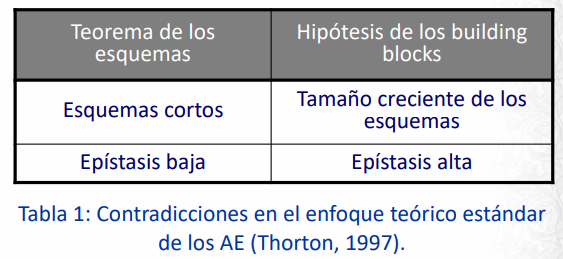
“Los esquemas cortos, de bajo largo de definición, cuyo fitness es superior al del promedio de la población, tienen una tasa decrecimiento exponencial. El AG hace este trabajo en un modo implícitamente paralelo para todos los esquemas de la población” D. Goldberg, 1989

Se prueba que el número de esquemas procesados para una población es del orden \(O(n^3)\) por lo que se procesa una gran cantidad de esquemas a pesar de manejar una cantidad relativamente baja de individuos. Se dice que un AG tiene la capacidad de paralelismo implícito: Capacidad del AE de explorar en forma simultánea múltiples secciones del espacio de búsqueda.

Se dice que los esquemas cortos con fitness superior al promedio y largo de definición se denominan building blocks, Los building blocks son los bloques básicos que el algoritmo genético combina para construir soluciones casi-óptimas para el problema de optimización.

Se critica el planteo de Goldberg Holland por ser medio cualquiera. Ya que para problemas deceptivos la idea de los building blocks no funciona (¿qué pasa si cuando junto una solución con otra solución buena obtengo una peor? No hay building blocks en realidad...).

Analisis de Whitney

Este autor se manda a estudiar el UX, muestra que no tiene sesgo y que está muy bueno. Luego hace un estudio de los alfabetos y considera que un schema es válido si un muestreo de forma estadística comprueba su relevancia si supera una cota arbitraria.

Adicionalmente critica a Goldberg por suponer que \(c\) es constante para calcular el fitness de un schema y señala que no se toma en cuenta las pérdidas y ganancias de los esquemas al aplicar los operadores. Por lo tanto, puede ser útil para estimar la cantidad de esquemas en 1 o 2 generaciones, pero no más allá.

Whitney plantea un modelo exacto que permite calcular el comportamiento de cada individuo del espacio de búsqueda:

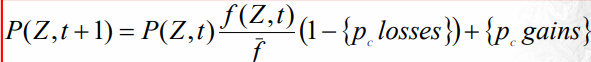
Todas estas ecuaciones son bastante complejas y poco útiles en la práctica. Otro problema de la teoría de los esquemas es que asume una epítasis baja. Donde epítasis[GT1] es el hecho de que la modificación de un gen afecta la probabilidad de que otros se alteren. Por ejemplo, en SPX, los genes que están juntos hay más chances de que sigan estando juntos que los que están bien lejos por como funciona SPX.

Se considera que el argumento de los building blocks es una falacia. ¡Ya que por un lado los building blocks son esquemas que se van agrandando por soluciones buenas, y por otro lado las soluciones grandes casi no tienen chances de sobrevivir!

A su vez no toma en cuenta restricciones, solamente codificación binaria y no garantiza la obtención del optimo.

Análisis de Markov

Tenemos un grafo donde cada estado es el conjunto de posibles individuos. Las transiciones a los estados son los operadores de cruzamiento y mutación que pueden generar las posibles poblaciones con sus probabilidades asociadas. De esta forma, aunque gigante, ¡tenemos todo el problema modelado y es finito! La cadena no es irreductible si solo hay operadores de selección y cruzamiento: ya que tiene estados absorbentes. Si no es elitista existe una probabilidad no nula de que el estado absorbente que converja no sea optimo.

De esta forma podemos obtener dos resultados:

1. Para algoritmo evolutivo no elitista: Si se agrega un estado de mutación no nos quedan estados absorbentes. – Bajo estas hipótesis el conjunto de estados generados será muy parecido al conjunto de estados originalmente planteados

2. : algoritmo evolutivo elitista. si se incorpora elitismo conservando la mejor solución se muestra que hay un solo estado absorbente que incluye a todas las poblaciones que tienen la solución óptima. ¡Por lo que para un número de generaciones finitas vamos a llegar a ese estado!

Resumen:

Otros Modelos

MOSES

Mutation Or selection evolutionary strategy (2001). Es un algoritmo evolutivo que no utiliza cruzamiento. Esto simplifica el mecanismo y permite realizar un análisis teórico de convergencia. Es parecido un poco al simulated annealing. El mecanismo de exploración se basa en una técnica estocástica Markoviana.

Las transiciones a de la cadena de markov asociada están dadas por el operador de mutación y su probabilidad asociada.

Inicializar la población
Mientras no se cumpla el criterio de parada
    - Hallar el mejor individuo I
    + = min{ f(In), n=1…k }
    - Sortear un entero z(0,k] según una ley binomial
    (k,e (-1/T))
    - Mutación: para los individuos Ir, r=1...Z cambiar
    Ir por Iq
    - Selección elitista: para los individuos Ir,
    r=z+1...k cambiar Ir por I
    +
Fin
Retornar I

La probabilidad de mutación no es constante, sino que depende del Diámetro del grafo de estados (diámetro = largo del camino más largo). El elitismo asociado permite la convergencia del algoritmo MOSES.

Tenemos 3 variantes:

1. Tradicional: Realiza sorteo binomial de z. \(p_mut\) es escalonado y los individuos tienen un orden fijo
2. No ordenado: No hay sorteo en z y la mutación se aplica de forma independiente: \(p_mut = e^{(-1/T)}\)
3. Ordenado: Los individuos se ordenan según su fitness. La mutación se aplica de manera independiente a cada individuo.

CHC

CHC es el acrónimo para: Cross generational elitist selection, Heterogeneous recombination and Cataclysm mutation.

Utiliza una estrategia elitista, un mecanismo de restricción al cruzamiento para individuos similares, no utiliza mutación, utiliza un operador de re-inicialización cuando se detecta una situación de convergencia.

Inicializar(Población)
Inicializar distancia
mientras (no criterio parada) hacer
    padres = selección (Población)
    if distancia(padres)  distancia then
        hijos = HUX (padres)
        newPob = reemplazo(hijos, Población)
    fin
    si (newPob == Población)
        distancia--
    Población = newPob
    si (distancia == 0)
        re-inicialización (Población)
        inicializar distancia
    fin
fin
retornar mejor solución encontrada

El operador HUX es el de medio cruzamiento uniforme (cada hijo tiene exactamente mitad y mitad de bits de los padres). La re-inicialización se realiza tomando como patrón al mejor individuo encontrado y haciendo un mecanismo de handshaking. Se reinicializa a un porcentaje de la población, es un parámetro a definir.

Al proporcional mayor diversidad genética, es capaz de obtener resultados superiores a los del AG tradicional para problemas “difíciles” (con espacio de búsqueda muy disperso, con funciones de fitness cuyos óptimos locales son muy atractores, etc.).

Algoritmo de estimación de distribuciones

Es un tipo especial de AE que no utiliza ni cruzamiento ni mutación. Es para problemas con números reales. En la generación t + 1, la población se construye realizando un muestreo probabilista de la población en t (o incluyendo memoria de las situaciones en t – 1, t – 2, etc.). La idea es modelar las interacciones entre las variables del problema de forma implícita (a diferencia del AE tradicional que las relaciones están implícitas en el procesamiento de los esquemas). Para problemas complejos es virtualmente imposible modelar todas las distribuciones de probabilidad posibles, ya que las interacciones entre variables se expresan de forma explícita en distribuciones de probabilidad conjunta que involucran a \( { x_i } \)

Inicializar (Población) t = 0 Mientras no se cumple la condición de parada { Selección de n individuos // n < #Población Hallar un modelo M que estime la distribución de probabilidad para las interacciones Generar Población en t + 1 muestreando sobre M } Retornar mejor solución hallada

Existen 3 formas para construir el modelo M: Análisis univariado, bivariado y multivariado.

El univariado es un modelo simple, no se considera relaciones entre variables. Las probabilidades se factorizan como producto de distribuciones marginales univariadas en independientes:

\[ P(x_1,x_2,\dots,x_n) = \Pi_{i=1}^{i=n} P(x_i) \]

En el bivariado se trabaja con probabilidades condicionales entre dos variables. Al estilo \(P(x_j | x_i)\) + un grafo de dependencia que muestra las restricciones entre dos variables.

El multivariado es el más complejo, los modelos son de orden N y se utilizan redes bayesianas/neuronales para su implementación.

Algoritmos Híbridos

Son aquellos que incluyen conocimiento específico del problema para mejorar el mecanismo de exploración del espacio de soluciones. También refiere a la combinación de técnicas de resolución para resolver un problema.

Fuertes

Los híbridos fuertes incluyen conocimiento específico del problema a resolver en la codificación o en los operadores específicos. Aumenta la eficacia, pero la formulación pasa a ser dependiente del problema.

Débiles

Combinan dos o más técnicas de resolución. Por lo general consiste en que una o varias técnicas específicas actúan como subordinadas de una maestra (El AE). Un ejemplo de esto es la combinación de AE con Simulated annealing como operador de búsqueda estocástica, llevando al algoritmo GASA.

Algoritmos Meméticos

Estos algoritmos híbridos incorporan conocimiento y combinan estrategias de búsqueda. Los memes son unidades de información que engloban ideas y conceptos de una sociedad. Los memes tienen un rol análogo a los genes, pero en la evolución cultural. La idea es incorporar conocimiento a través de memes que pueden ser útiles para hallar eficientemente las mejores soluciones.

Los individuos (agentes) tienen la capacidad de intentar mejoras, y compiten entre sí por propagar sus memes generando un mecanismo guiado de competición. Es decir, se crea una búsqueda local en base a los memes.

Puede aplicarse como un nuevo operador:

Selección (operador tradicional)
Cruzamiento (operador tradicional)
Mutación (operador tradicional)
Búsqueda memética iterada

O como una modificación de un operador evolutivo:

Selección (operador tradicional)
Cruzamiento memético
Mutación memética (o búsqueda memética)

' Características de los algoritmos memeticos:

Algoritmos Paralelos

HPC (High Performance Computing)

El procesamiento paralelo es una forma eficaz de procesamiento de la información que favorece la explotación de los sucesos concurrentes en el proceso de computación. Varios procesos cooperan para resolver un problema en común. Tenemos dos tipos:

1. Procesamiento paralelo: Procesos concurrentes ejecutando en un mismo computador o computadoras interconectadas localmente. Tiene una mayor capacidad y tiempo de proceso y aprovecha la escalabilidad potencial de los recursos.

2. Procesamiento Distribuido: Procesos concurrentes ejecutando en forma distribuida en varios computadores no localmente interconectados. Mayor desempeño y robustez a fallos. Es más problemático el tema de seguridad y acceder a datos no locales.

Estos modelos escapan a la arquitectura tradicional de Von Neumann. La siguiente categorización de arquitecturas de Flynn:

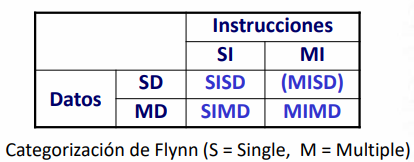
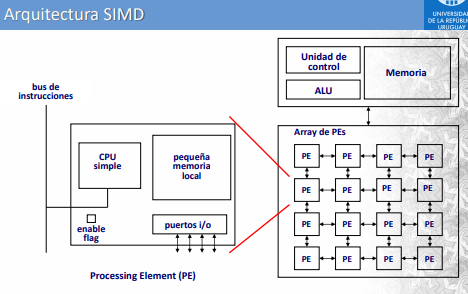
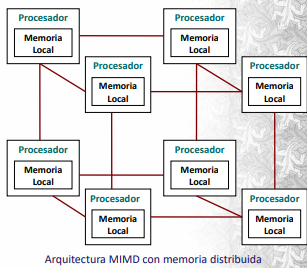
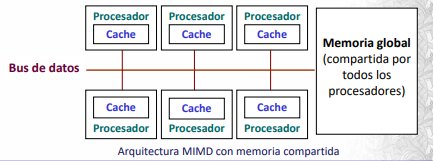
La computación paralela utiliza arquitecturas de tipo SIMD y MIMD. La SIMD consiste de un único programa que controla muchos procesadores. Por otro lado, la arquitectura MIMD consiste en varios procesadores que actúan de manera asíncrona y se debe explicitar la sincronización. LA comunicación se realiza a través de memoria compartida o distribuida.

Cuando la memoria es compartida el bus de datos actúa como cuello de botella. La memoria distribuida utiliza la sincronización a través del pasaje de mensajes. Es mucho más escalable y apropiada para decenas de miles de procesadores.

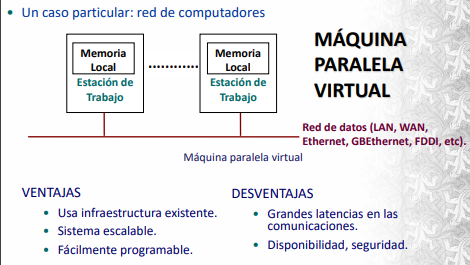
Un ejemplo de MIMD implícitamente popular son las maquinas paralelas virtuales:

Para evaluar el desempeño de un algoritmo paralelo se usan las siguientes métricas:

1. Speedup absoluto: \(SN = T_0 / T_N \) Donde \(T_0\) es el tiempo del algoritmo serial más rápido y \(T_N\) el tiempo del algoritmo paralelo ejecutado en N procesadores.

2. Speedup algoritmo: \(S_N = T_1 / T_N \) Donde \(T_1\) es el tiempo de ejecución del algoritmo en forma serial y \(T_N\) el tiempo del algoritmo paralelo en N cores.

Se suele usar el speedup algorítmico ya que el absoluto es difícil de calcular. La situación ideal es alcanzar un speedup lineal, aunque no siempre es posible.

La eficiencia computacional se define como \(E_N = T_1 / (N \times T_N)\) . Valores de eficiencia cercanos a uno indican mejoras casi ideales de desempeño. Otro factor importante es la escalabilidad, la cual es la capacidad de agregar procesadores para obtener un mejor rendimiento.

Algoritmos Evolutivos Paralelos (PEA)

Se aplican técnicas de paralelismo con el afán de mejorar la eficiencia (paralelar fitness, por ejemplo) y mejorar la calidad del mecanismo de búsqueda genética. La idea es aprovechar el paralelismo intrínseco del mecanismo evolutivo, trabajando simultáneamente sobre viarias poblaciones.

Existen 3 formas diferentes de organizar la población:

1. Maestro/Esclavo: Asigna procesadores distintas etapas del mecanismo evolutivo. Por lo general se distribuye la evaluación del fitness la cual suele ser costosa.

2. Subpoblaciones distribuidas: ES un enfoque orientado a distribuir los datos en poblaciones semindependientes

3. Celular: Trabaja con la estructura espacial subyacente que ordena a los individuos de la población.

A excepción del master/slave, los otros 2 modelos tienen un comportamiento algorítmico diferente. Think about it...

A su vez aparecen nuevas tuercas que podemos ajustar en un modelo paralelo:

• Evaluación del fitness: Concentrada o compartida
• Nro de poblaciones: panmixia o poblaciones múltiples
• Mecanismo de intercambio entre poblaciones
• Mecanismo de sincronizaron entre elementos
• Cruzamiento centrado o distribuido
• Selección aplicada a conjuntos locales o globales.

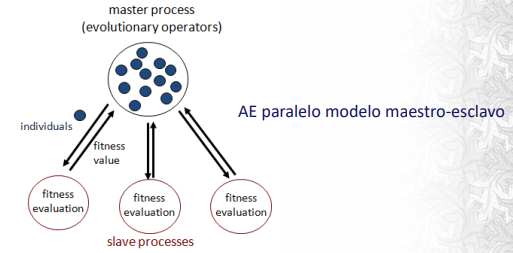
Master / Slave

Estructura jerárquica donde maestro controla la búsqueda y esclavos hacen la tarea subordinada (ej computar fitness). La evolución es panmíctica. Muy efectivo para mejorar la eficiencia computacional de problemas complejos.

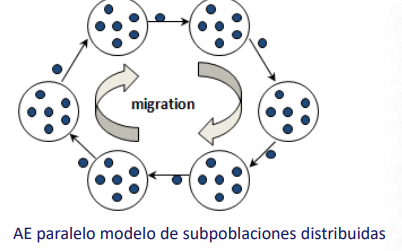
Subpoblaciones distribuidas

Se distribuye la población en subpoblaciones (“islas” o “demes”), que evolucionan de modo semindependiente. Hay un operador de migración que comunica material genético entre las islas. Cada isla opera con la lógica de un AE secuencial y son independientes. La diversidad provista por las múltiples islas y la migración le permiten a esta variante obtener resultados de mejor calidad que un AE secuencial.

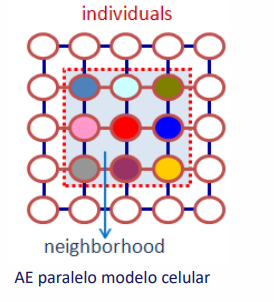
Modelo Celular

Los individuos se ubican en una estructura espacial subyacente. Se usa un operador de difusión para la transmisión de características. Lo cual es un modelo local de evolución restringido a las vecindades. El mecanismo de interacción restringido por la estructura espacial subyacente y la lenta propagación de características constituyen una técnica efectiva para preservar diversidad en las soluciones de la población. Adecuado para computadoras de tipo SIMD.

Adicionalmente tenemos los modelos híbridos que combinan todos estos modelos. A su vez existen múltiples bibliotecas de desarrollo disponibles públicamente que encapsulan las funcionalidades necesarias para implementar AE paralelos.

AE Multiobjetivo

Las principales características de un problema MOP (Multiobjective Optimization Problem) son:

1. Espacio multidimensional de funciones
2. No existe una única solución al problema
3. Es necesario un proceso de toma de decisiones en la cual se decide qué tipo de compromisos son más convenientes desde la perspectiva de quien toma las decisiones. Esto último puede ser a priori o a posteriori.

Formulación:

\[ Min/Max \ F(x)=(f_1(x),\dots,f_n(x)) \ sujeto \ a \ G(x)=(g_1(x),\dots,g_n(x)) \geq 0 \ sujeto\ a\ \ \ \dots \ \dots \]

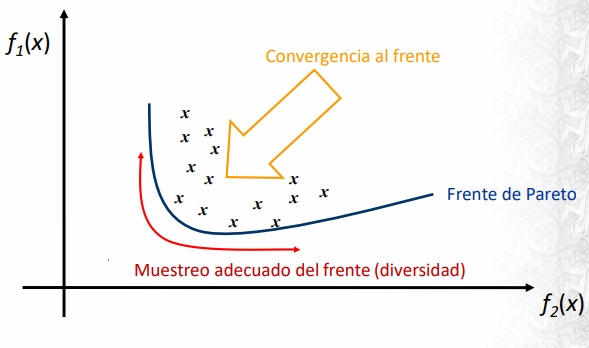
Como consecuencia la noción de optimo se modifica. Se le llama óptimo de Pareto a una solución que no existe ningún vector factible que sea mejor en algún criterio sin empeorar otro. De Wikipedia:

• Given an initial situation, a Pareto improvement is a new situation where some agents will gain, and no agents will lose.
• A situation is called Pareto dominated if there exists a possible Pareto improvement.
• A situation is called Pareto optimal or Pareto efficient if no change could lead to improved satisfaction for some agent without some other agent losing or if there is no scope for further Pareto improvement.

The Pareto frontier is the set of all Pareto efficient allocations, conventionally shown graphically. It also is variously known as the Pareto front or Pareto set. La dominancia de Pareto es una relación de orden parcial.

Los algoritmos evolutivos multiobjetivo se les llama MOEA (MultiObjetve Evolutionary Algorithm). Son una técnica muy moderna la cual hay mucha investigación en estas últimas décadas.

Las ventajas de usar un AE para multiobjetivo es que al trabajar con poblaciones pueden capturar ese frente de Pareto de forma más natural, son menos sensibles a la continuidad del FP y permiten abordar problemas multidimensionales con gran naturalidad. El objetivo de un MOEA es entonces aproximar este frente de Pareto, muestreándolo adecuadamente y hacerlo de forma computacionalmente eficiente.

Esquema algorítmico:

Inicializar(P(0))
generación = 0
mientras (no CriterioParada) {
    Evaluar(P(generación))
    Operador de diversidad(P(generación)) (!!!)
    Asignar fitness(P(generación)) (!!!)
    Padres = Selección(P(generación))
    Hijos = Operadores de Reproducción(Padres)
    NuevaPop = Reemplazar(Hijos,P(generación))
    generación ++
    P(generación) = NuevaPop
} retornar frente de Pareto

Los operadores característicos de los MOEA son el operador de diversidad y de asignación de fitness. El primero aplica una técnica para evitar la convergencia en un solo sector del frente de Pareto. La asignación de fitness está orientada a perpetuarse a aquellos individuos con mejores características.

Existen dos propuestas de MOEA:

1. Non-pareto based MOEA: Mecanismos de fitness sencillos que no reflejan independencia de objetivos del problema y no garantizan la correcta resolución del MOP

2. Pareto based MOEA: Utilizan dominancia de Pareto para el proceso de asignación de fitness.

Non-Pareto MOEA

Son adecuados para problemas con no más de 3 funciones objetivo y espacio de soluciones sencillo. Existen varias propuestas de mecanismos de asignación:

La clásica combinación lineal de objetivos: \(F(x) = \sum w_i . f_i(x)\) . No refleja el carácter multiobjetivo del problema.

El ordenamiento lexicográfico trata de optimizar las funciones en un orden de jerarquía. Y la \(\epsilon\) - constraint optimiza funciones objetivo considerando como restricciones acotadas por ciertos niveles permisibles (eps).

Después está el target vector que trata de alcanzar un vector ideal mediante la combinación de estrategias. Goal attainment: Busca alcanzar metas definidas a priori por el usuario.

Pareto based MOEA

Los pareto based usan mecanismos para preservar la diverstiy. Los más usados son:

• Fitness sharing: Se fija la distancia con otras soluciones del frente de Pareto.
• Restricción al cruzamiento: Impide combinación de individuos similares
• Crowding: No tener todas las soluciones en un sector
• Otros: Isolation by distance.

La primera generación de MOEAS son: NSGA, NPGA y MOGA. Se caracterizaban por utilizar dominancia de Pareto, nichos y sharing para proveer diversidad y no usaban elitismo.

La segunda generación de MOEAS son: SPEA, SPEA-2, PAES, NSGA–2, NPGA–2 y MICRO-GA. Se agrega elitismo con los modelos \((\mu+\lambda)\) o población externa.

SPEA y SPEA2

Utiliza población externa. Se basa en el concepto de fuerza, la cual es proporcional al número de individuos que son dominados por él. Se utiliza clustering para mantener la diversidad. El SPEA-2 actualiza la función de fitness para también tomar en cuenta los individuos que domina, agrega estimaciones de densidad de individuos destino y utiliza un esquema de truncamiento para preservar las soluciones frontera.

PAES

Utiliza un archivo histórico de individuos no dominados. Realiza una división del espacio de funciones generando una grilla adaptativa, a esta se le aplica técnicas de crowding.

NSGA2

Elitismos vía mu+lambda. Aumenta la eficiencia computacional (reemplaza el sharing del NSGA por crowding) y da muy buenos resultados para representaciones reales.

Micro-GA

Se caracteriza por utilizar una población muy pequeña e incorporar un mecanismo de re-inicialización cuando se alcanza la convergencia. Utiliza dos poblaciones, una reemplazable y una no reemplazable con la cual se maneja la dominancia y la diversidad. La incorporación del elitismo se basa en la idea de mantener soluciones no dominadas, pero con una memoria que se actualiza a plazos.

Métricas para evaluar MOEAs

Las métricas deben evaluar:

• la calidad de los resultados (cercanía al frente de Pareto).
• la diversidad de las soluciones encontradas.
• la cantidad de elementos del conjunto de óptimos de Pareto.
• la eficiencia computacional del algoritmo.

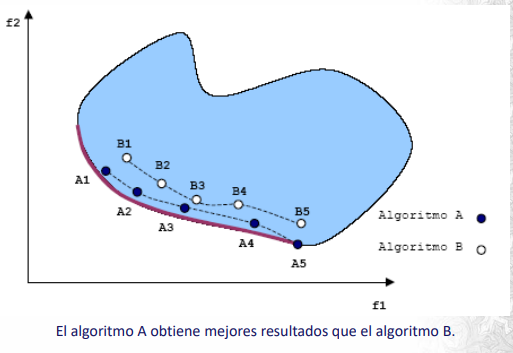
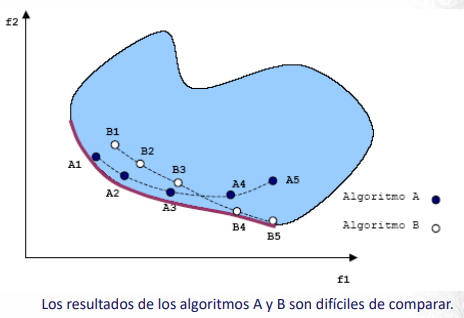
Algunas de estas métricas son:

Número de puntos no dominados: Cantidad de puntos no dominados que encuentra el algoritmo.

Tasa de error: Indica el porcentaje de soluciones que no son miembros del frente de Pareto. Es decir, requiere conocer el frente de Pareto o saber determinar si un punto lo está o no. \(ER = sol_pareto / n \)

Distancia generacional: Busca estimar qué tan lejos están los elementos no dominados obtenidos como resultado de los elementos del verdadero frente de Pareto. Siendo p la dimensión del espacio:

\[ GD = \frac{(\sum d^p_i)^{1/p}}{n} \]

Spacing: Evalúa la distribución de los puntos no dominados hallados como solución del problema mediante el MOEA:

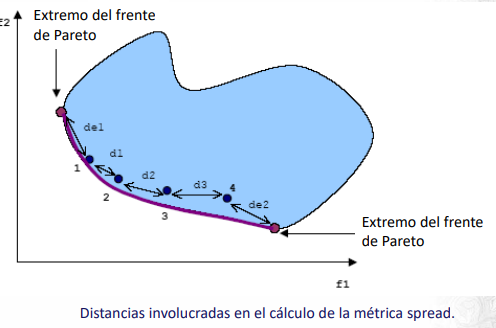
\[ SP = \sqrt{\frac{1}{n-1} \sum^n_{i=1} (\bar{d}-d_i)^2} \]

Donde \(d_i\) mide la distancia en el espacio de las funciones objetivo entre la solución i-esima y su vecino no dominado más próximo. \(\bar{d}\) es el promedio de los \(d_i\)

Spread: Utiliza como información adicional a spacing la distancia a los “extremos” del frente de Pareto, aquellos puntos con menores valores en cada una de las funciones objetivo, para tener una medida más precisa de la cobertura del frente.

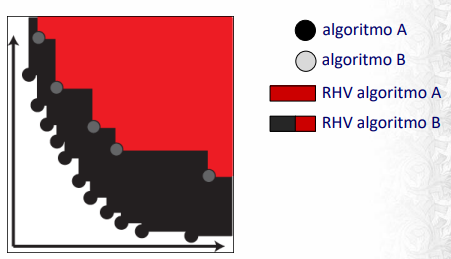
Hipervolumen relativo (RHV) : Cociente entre el volumen (en el espacio de funciones objetivo) cubierto por el frente de Pareto calculado por el algoritmo y el volumen cubierto por el frente de Pareto real.

Empirical attainment surface (EAS): Estimador estadístico de la métrica attainment surface, que estima para cada vector en el espacio de funciones objetivo la probabilidad de ser dominado por el frente de Pareto calculado en una ejecución individual del MOEA evaluado.

Evaluación Experimental AEs.

Objetivos de la Ev.Experimental

Los algoritmos evolutivos no son deterministas, por lo que es necesario realizar una evaluación estadística de los resultados obtenidos a partir de un conjunto de ejecuciones diferentes. Por ello es importante tener una cantidad de ejecuciones independientes significativa (en simples se recomienda 50, 30 en complejos).