The craft of functional programming notes

With functional programming languages, it is so much easier to test... Test suits or randomly generated data don't give full assurance that a program will never go wrong. A proof does.

The Haskell development platform includes:

• GHC: The Glasgow Haskell Compiler
• GHCi: The interactive version of GHC
• Cabal: Sth for importing libraries
• Haddock: For writing docs

GHCI includes commands prefixed by ":". For instance,: reload reloads the file that have been loaded to ghci if modified.

Some nice commands:

• load file
• info name --get information about name
• browse name --browse the definitions in a file called name.hs
• quit
• ! cmd --execute an UNIX command
• edit file.hs --edit a file. Hs is needed
• let s = exp --define a variable for ghci runtime

To make programs manageable we use modules to divide it in smaller components. A module has a name and a collection of definitions.

A Haskell module begins with:

module MODULE_NAME where

and to import one we write:

import MODULE_NAME

importing means we can use the definitions from other modules in the module we are writing.

Expressions like 2 or True are called literals because the result of evaluating them is the literal itself.

Observe the precedence of operators: This is interpreted as negate minus 34: negate -34. Parenthesis should be applied.

maxBound gives the value of the maximum Int.

Many functions and operators are overloaded in Haskell. The function == carries the signatures Int -> Int -> Bool and Bool -> Bool -> Bool for example.

To hide functions min, max defined in the prelude you can use the line:

import Prelude hiding (min, max)

The standard library Data.Char contains many functions for handling chars lick isDigit or toUpper.

To print characters into the screen we have the primitive Haskell function putStr :: String -> IO () which has the effect of putting the argument string on the screen.

String can be concatenated using the operator "++" so "pog"++"ger"++"s"="poggers".

The functions show and read we can convert values to string and vice versa. In the situations when the return value of a function is not clear you can give a proper output type by:

(read "3") :: Int -- This will output an Int

Haskell supports scientific notation for floats. For instance: 231.61e7 = 2 316 100 000

Haskell indentation uses the offside rule. When you write a definition it creates a box. It is expected that everything written in the box forms part of the definition

The textbook recommended layout for long definitions is:

fun v1 v2 ... vn | a long guard... go over a number of lines = very long expression which goes over a number of lines | g2 = e2 | ...

An example of writing out of the box which gives a parsing error:

funny x = x+ 1

The names used in definitions of values must begin with a small letter, as must variables and type variables. Capital letters at the beginning are reserved for type Names (Int), constructors, and type classes.

Haskell is built on top of the Unicode. So, you can write whatever you want without prejudice. Unicode characters can be inputted as a 16-bit sequence in the form \uhhh.

In Haskell each non associative operator is classified as either left or light associative. For instance, '-' is left-associative:

4-2-1 evaluates to (4-2)-1.

When we have expressions with different operators we have to compare it’s binding power for instance * has binding power 7 while + has 6, and ^ 7.

Binding most tightly is function application. I.e., f n +1 binds to f(n_+1.

Haskell lets you define our own infix operators. Operator names are built from the operator symbols like !,#,%,+,.,/,<,=,~,etc.

For instance, for defining the operator x &&& y we write:

(&&&) :: Integer -> Integer -> Integer x &&& y | x > y = y | otherwise, x

Chapter 4: Designing and writing programs

Design is what we do before we start writing detailed Haskell code.

What if I had any functions I wanted? Which could I use in writing the solution?

The latter is the so-called top-down approach: We work by breaking a problem into smaller individual problems.

Dividing a function into local definitions using where is a key principle in programming with Haskell. The let expression let a; b; c; in f is also used occasionally.

The recommended indentation for local functions is:

f p1 p2... pk | g1 = e1 | ... | otherwise = er where v1 a1 an = r1 v2 = r2 ....

It is also possible to include the signature of local functions, and it is suggested when the locally defined object is not obvious.

Scope

You can use definitions that are declared before in the script when you are writing new functions.

When using a quickCheck with custom data. We need to define an Arbitrary constructor:

instance Arbitrary DataType where dataType = elements [e1,e2,...,en]

Deriving sth gives the datatype additional capabilities. Deriving Ord, lets you use <'s operators, Eq the == and Show functions to print the Enum on screen. The Ord is given by the order of elements when they are defined.

You can give string errors in Haskell by writing error "msg". For example: f n | n==0 = 0 | n<0= error "n has to be 0"

Testing

The art of testing is then to choose the inputs to be as comprehensive as possible. That is, we want to test data to represent all the different ‘kinds’ of input that can be presented to the function.

Como elegimos los datos de prueba? Existen dos approaches. Uno es mirar la especificación del programa y hacer tests en base a esto (black box) el otro es mirar como está hecho la función y hacer las pruebas con esto en mente (White box testing).

Chapter 5: Data types; tuples and lists

In a tuple, we combine a fixed number of values of fixed types – which might be different – into a single object. In a list we combine an arbitrary number of values – all of the same type – into a single object.

Tuples

Podemos nombrar un tipo tuple de la siguiente manera

type ShopItem = (String, Int)

Para declarar que algo es de un type en particular:

("Salt: 1kg",139) :: ShopItem

Los items de una lista se pueden escribir como:

type Basket = [ ShopItem ] type String = [ Char ]

Es importante que las listas sean siempre del mismo tipo para mantener la propiedad de type checking previo a ejecución.

Las tuples son útiles para retornar varios "valores" desde una función.

Haskell implementa pattern matching para las tuples. Por ejemplo:

addPair :: (integer, Integer) -> Integer addPair (x,y) = x+y

addPair :: (integer, Integer) -> Integer addPair (0,0) = 0 addPair (0,y) = y addPair (0,x) = x addPair (x,y) = x+y\

Se aplican las reglas clásicas del Pattern Matching.

Adicionalmente para las 2-úplas (x,y), existen las funciones selectoras fst y snd . However, this is discouraged.

fst (x,y) = x snd (x,y) = y

Se deben definir funciones selectoras para poder acceder a los elementos de las tuplas.

Algebraic Types

Un tipo algebraico vendría a ser un struct de c. Se introducen con el keyword data, les sigue su nombre y un igual con la información de como se construyen estos elementos.

Estructura de un tipo algebraico:

data name = C_1 a_1 ... a_1k | ... C_n a_n ... a_nk

Donde C_n es un constructor. Los nombres de type y los constructores comienzan con mayúsculas.

Product type

Se le llama al tipo de dato algebraico que tiene un numero arbitrario de campos de tipo type. Por ejemplo:

data People = Person Name Age deriving (Eq,Show) donde: type Name = String type Age = Int

A los constructores se les puede aplicar pattern matching:

data Shape = Circle Float | Rectangle Float Float deriving (Eq,Ord,Show)

area :: Shape -> Float area (Circle r) = pi * r * r area (Rectangle h w) = h * w

Es importante notar que podemos ponerle el mismo nombre a un tipo de dato algebraico y a un constructor, pero esto es extremadamente confuso por lo que se sugiriere evitarlo.

Podemos entender los constructores como funciones que construyen el objeto Shape:

Circle :: Float -> Shape Rectangle :: Float -> Float -> Shape

Es importante subrayar la diferencia entre type y data. El primero es un sinónimo, se puede escribir de la manera larga y es prescindible del programa. Por otro lado, un data no. Es un nuevo tipo de dato que antes no existía. Más adelante se verá que los tipos algebraicos pueden ser recursivos y polimórficos.

Lists

A list in Haskell is a collection of items from a given type. For every type t there is a Haskell type [ t ] of lists of elements from t.

[’a’,’a’,’b’] :: String
"aab" :: String

También podemos tener listas de funciones, o listas de listas:

[fastFib,fastFib] :: [ Integer -> Integer ]
[[12,2],[2,12],[]] :: [ [Integer] ]

A su vez, la lista vacía representada como [] pertenece a todos los tipos de listas.

Las listas de tipos enumerados (integers, chars, etc.) pueden escribirse con notaciones especiales:

[n .. m] is the list [n,n+1,...,m]; if n exceeds m, the list is empty:
[3.1 .. 7.0] -> [3.1,4.1,5.1,6.1,7.1]
[’a’ .. ’m’] -> "abcdefghijklm"

[n,p .. m] is the list of numbers whose first two elements are n and p and whose
last is m, with the numbers ascending in steps of p-n. For example,
[0.0,0.3 .. 1.0] -> [0.0,0.3,0.6,0.8999999999999999]
[’a’,’c’ .. ’n’] -> "acegikm"

Strings

Los strings se concatenan con el operador ++. Existen las funciones show y read que permiten imprimir un string y leer de un string respectivamente. Cuando no es claro cual es el resultado de la función read, se puede aclarar realizando:

(read "3") :: Integer

List Comprehensions

In a list comprehension we write down a description of a list in terms of the elements of another list.

Primero, tenemos un generador de onde provienen los elementos de la lista, luego tenemos multiples tests para saber si incluir o no un elemento generado, por ultimo los elementos que pasan los test se transforman.

Ejemplos: ex = [1,2,3] [2*n | n<-ex] -> [2,4,6] [n+1 | n<-ex, isEven n] -> [3]

También podemos aplicar técnicas de pattern matching sobre el generador:

addPairs :: [(Integer,Integer)] -> [Integer]
addPairs list2 = [m+n | (m,n)<-list2, m>0]

Observar que una list comprehension puede formar parte de la definición de una función:

allEven xs = (xs == [x | x<-xs, isEven x])

De la misma manera que el patrón del generador no tiene que hacer matching de todos los elementos de la lista, así excluyéndolos:

circles :: [Shape] -> Int
circles shapes = sum [1 | Circle r <- shapes]

Chapter VI: Programming With Lists

En haskell las funciones pueden ser polimórficas. Estas funciones se ven acotadas por su forma.

At work here is the principle that a function’s type is as general as possible, consistent with the constraints put upon the types by its definition.

Ejemplos de declaraciones polimórficas:

a -> b -> a
[a] -> a -> (a,[a])
a -> Int -> b

Se dice que una signature es una instancia de una más general si obedece su forma polimórfica.

Se puede obtener el tipo de una función escribiendo :type f en GHCi.

Es importante aclarar que el polimorfismo y la sobrecarga son dos cosas distintas. Una función polimórfica tiene una sola definición, mientras que la sobrecarga son varias declaraciones de funciones con el mismo nombre para distintos tipos de datos, y por ello son funciones distintas.

Haskell functions: Prelude

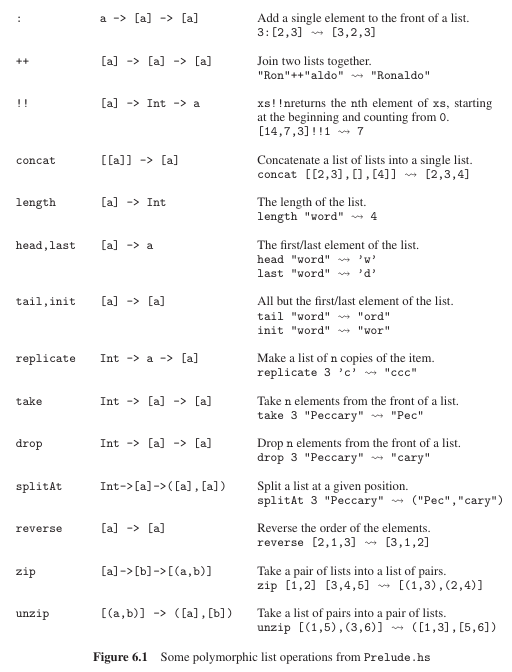
En Haskell se tiene por convención que los nombres de los módulos tengan un orden jerárquico utilizando palabras separadas por puntos y con letra capital. Las palabras más a la izquierda son las jerarquías más superiores.

Muchos módulos de Haskell importan todos sus sub-módulos hijos, por ejemplo Foreign.C importa Foreign.C.(Types,String,Error)

Las librerías más importantes de Haskell son:

• Prelude: La librería estándar, viene importada por defecto.

• Control: Control.Monad contiene definiciones para operar IO en Haskell, así como operaciones con side-effects.

• Foreign: Librerías para soportar la ejecución de programas escritos en otros idiomas.

• Numeric: Funciones para leer/escribir números en varios formatos

• System: Handling de I/O, System Calls, interacción con sistema UNIX.

The Haskell Platform es un bundle de GHC que incluye varias herramientas estándar (incluyendo GHCi).

HackageDB es el repositorio de módulos de Haskell más importante.

Existe un sistema para generar documentación de módulos llamado Haddock.

Cabal

Cabal es una herramienta para instalar paquetes y sus dependencias. Los comandos más importantes son:

• cabal update: Actualiza los paquetes disponibles
• cabal list s: lista los paquetes cuya descripción contengan s.
• cabal install pkg: Instala la última version del paquete pkg
• cabal install pkg-1.0: Instala la versión 1.0 de pkg
• cabal install pkg <2: Instala una version de pkg anterior a la 2.0
• cabal install pkg --dry-run : Instala pkg a ver qué pasa, no se hace efectivo el cambio.
• cabal help
• ghc-pkg list: Lista todos los paquetes instalados

Mucha de la documentación de los paquetes se encuentra disponible en Hackage. Existen herramientas de búsqueda de funciones y módulos como Hoogle

Chapter VII: Defining functions over lists

Pattern Matching II

El símbolo wildcard se utiliza para hacer matching de cualquier cosa, se utiliza para no asignarle un nombre al patrón. Ejemplo foo 0 y = y foo x _ = x

Un patrón puede estar compuesto por:

1. Un valor literal. Por ejemplo: 24, 'f', True.
2. Una variable: x,y ...
3. Un wildcard: _ . Matches cualquier valor
4. Patrón tuple: (p_1,..,p_n). Matches tuples de valor (v_1,..,v_n) donde cada v_k matches p_k
5. Un constructor aplicado a un numero de patrones (C p_1 p_2 ... p_n). Esto fuerza que el valor haya sido construido por C y cada argumento v_k matches p_k

Recordar nuevamente que los patrones se evalúan de manera secuencial.

List Patterns

[] es la lista vacía. Las listas no vacías tienen un head y un tail, head es el primer elemento y tail es el resto de la lista si se le quita dicho elemento. A su vez, las listas tienen un constructor elemental llamado cons que se escribe ":"

  (:) :: a -> [a] -> [a]]
(:) x xs ---> [x]++xs

Cons tiene la propiedad interesante de que toda lista tiene una única forma de ser construida con el operador cons. Esto no se cumple, por ejemplo, con el operador de concatenación ++.

Algunos ejemplos de pattern matching clásicos con estas listas son:

• (x:_) : matches el head de la lista y el resto de la misma
• (_ : _) : matches cualquier elemento excepto la lista vacía

Recordar que la función tiene precedencia al cons, por lo que f x:xs != f (x:xs).

A list will match the pattern (p:ps) if it is non-empty, and also if its head matches the pattern p and its tail the pattern ps.

Nota: No se puede hacer chequeos de igualdad en el pattern matching. Por ejemplo, el siguiente patrón no es válido en Haskell: x (x:ys)

Case expression

Utilizamos case para hacer pattern matching de varios casos. Similar a las guardas | pero en vez de evaluar una condición se realiza el primer caso en que el patrón coincide.

En forma general:

case e of 
  p1 -> e1
  p2 -> e2
  ...
  pn -> en

Por ejemplo:

firstDigit :: String -> Char
firstDigit xs =
  case (digits xs) of
    [] -> '\0'
    (x:_) -> x

Recursión sobre listas

El uso de cons para la recursión sobre las listas es esencial. Esto junto al paso base de la lista vacía [] nos permite desarrollar cualquier esquema de recursión primitiva.

La idea de recursión es responder la pregunta:

What if we were given the value fun xs. How could we define fun (x:xs) from it?

Ejemplo: Insertion Sort

Algoritmo de ordenamiento clásico. Consiste en iterar sobre cada elemento y volver a iterar la lista asegurando que los números a la izquierda son más pequeños que el elemento fijado:

iSort :: [Integer -> Integer]
iSort (x:xs) = ins x (iSort xs)

ins :: Integer -> [Integer] -> [Integer]
ins x [] = [x]
ins x (y: ys)
  | x <= y = x:(y:ys)
  | otherwise = y : ins x ys

Ejemplo: Quicksort

It is striking to see how close this program is to our informal description of the algorithm, and this expressiveness is one of the important advantages of a functional approach.

qSort :: [Integer] -> [Integer]
qSort [] = []
qSort (x:xs) = (qSort [y | y<-xs, y<=x]) ++ [x] ++ (qSort [y | y<-xs, y>x])

Chapter VIII: I/O in Haskell

La solución al problema de I/O en Haskell se basa en introducir el type IO a . El cual se puede entender como un programa que realiza actividades de entrada/salida y luego retorna un valor de tipo a.

One way of looking at the IO types is that they provide a small imperative programming language for writing I/O programs on top of Haskell, without compromising the functional model of Haskell itself.

Las funciones clásicas de input son: getLine :: IO String y getChar :: IO Char.

Type ()

Haskell tiene el tipo () el cual contiene un solo elemento que se escribe (). Este valor no aporta información. Se utiliza para la signature de programas I/O para indicar que el resultado que retorna no tiene ninguna importancia. Por ejemplo: putChar :: Char -> IO ()

Main module

Al compilar un programa con GHC, este produce un ejecutable que ejecuta la función main :: IO t. Donde t es un tipo, usualmente (). Por defecto se espera que el programa main se encuentre en el modulo Main.

Hello World

putStr :: String -> IO ()
helloWorld :: IO ()
helloWorld = putStr "Hello, World!"

NOTA: Es importante destacar que GHCi embebe las ejecuciones de las funciones en el programa show. Por lo que cuando se muestra el resultado de las funciones, GHCi está embebiendo la función en un programa I/O de forma discreta.

Show

Los valores que se pueden imprimir en general son los que pertenecen a la clase Show. Por ejemplo, para decir que un tipo a debe pertenecer a dicha clase en la signature de una función: print :: Show a => a-> IO ()

Return

Para obtener el resultado de un programa I/O precisamos la función de Haskell return :: a -> IO a. La cual retorna el resultado a. Si escribimos return () esto es equivalente a no hacer nada, no se retorna ningún valor. Un uso de esto es:

if condition then action else return ()

Do

La estructura Do es el pilar fundamental para los programas estructurados en haskell. Permite secuenciar un programa I/O y nombrar (bind) valores retornados por acciones I/O.

Por ejemplo, para realizar varias acciones I/O en forma secuencial:

put4times :: String -> IO () put4times str = do str putStrLn str putStrLn str putStrLn str putStrLn

Para capturar un valor de un programa I/O se utiliza el operador <-:

getNPut :: IO ()
getNPut =
  do line <-getLine
    putStrLn line
  --line tiene el resultado de getLine!

El <- puede entenderse como el let que guarda un valor, ya que binds una variable un valor, pero luego este no se puede modificar. A su vez, los let clásicos se pueden utilizar con juicio para realizar definiciones locales:

readme :: IO ()
readme  =
  do lect <- readLine
    let toPrint = f lect
    putStr toPrint
    putStr toPrint

Es importante observar que el type de ch <- getChar es Char y el de let ch = getChar es IO Char.

Read

Haskell contiene la clase Read con la función read :: Read a => String -> a la cual sirve for parsing un string y obtener un valor. Por ejemplo, para obtener un entero desde la entrada:

getInt :: IO Integer
getInt = do line <- getLine
    return (read line :: Integer)

Loops

Los programas secuenciales en Haskell pueden ser iterativos mediante recursión. Por ejemplo:

copyN :: Integer -> IO ()
copyN n = if n <= 0 then return () else
  do
    line <- getLine
    putStrLn line
    copyN (n-1)

A las variables que se utilizan para controlar una recursión se les suele llamar loop data.

Chapter IX: Proofs

Uno de los aspectos interesantes de la programación funcional es la capacidad que nos proporciona para probar propiedades de las funciones que construimos. Es decir, podemos probar la correctitud de una función.

Para ello nos basamos fuertemente en el principio de inducción primitiva y general (PIP) y la manipulación simbólica.

Definedness, termination and finiteness

Evaluar una expresión tiene dos resultados. O la evaluación termina, dando un resultado o esta continúa evaluándose para siempre. Cuando una expresión no llega a un resultado decimos que es undefined, en el caso contrario defined.

La evaluación de Haskell es lazy, es decir, los argumentos de las funciones se evalúan solamente cuando su valor realmente se necesite. Este método de computación nos permite definir y utilizar infinite lists como [1,2,...] y partially defined lists . Las listas finite son aquellas de largo finito y elementos defined.

Chapter X: Patterns of Computation

Reutilizar el software es un objetivo importante de la programación. Haskell nos permite cumplir este objetivo mediante polimorfismo y patrones clásicos de filtrado/combinación junto a funciones de alto orden.

A function is higher-order if it takes a function as an argument or returns a function as a result, or does both.

Mapping

Este patrón se da cuando queremos aplicar una transformación a todos los objetos de una lista.

la función map de Haskell nos permite realizar mappings sin tener que nombrar funciones específicas para cada caso:

map :: (a -> b) -> [a] -> b
map f xs = [f x | x <- xs]

Observar que la notación (signature) nos permite definir el tipo función.

ZipWith

¿Existe un caso más general para la función zip? Notar el caso en que tenemos dos listas y queremos realizar operaciones sobre ella tomando un elemento de cada lista y aplicando una transformación. Para ello Haskell nos provee de la función zipWith:

zipWith :: (a->b->c) -> [a] -> [b] -> [c]
zipWith f (x:xs) (y:ys) = f x y : zipWith f xs ys
zipWith f _ _ = []

Filtering

Este patrón se da cuando queremos seleccionar los elementos de una lista que cumplen una propiedad.

Para ello definimos nuestra propiedad p :: a -> Bool. Por convención las propiedades suelen identificarse con el prefijo is. Aplicar el filtro consiste en utilizar la función filter:

filter :: (a -> Bool) -> a -> [a]
filter p [] = []
filter p (x :xs)
  | p x = x : filter p xs
  | otherwise = filter p xs

Folding

Este patrón se da cuando queremos computar una función utilizando los elementos de la lista.

Para ello utilizamos las funciones foldr y foldl de haskell. Estas son: foldr :: (a->b->b) -> b ->[a]-> b y foldl :: (b->a->b)->b->[a]->b. La primera empieza de la derecha, la segunda desde la izquierda.

Conceptualmente tienen un mecanismo distinto de funcionamiento:

Foldl es:

1. Left associative
2. Tail recursive
3. Lazy
4. Backwards

Foldr es:

1. Right associative
2. Recursive into the argument.
3. Lazy
4. Backwards

Existe una variante llamada foldl' que implementa un fold estricto (se evalua en seguida el argumento). Lo cual es util para mejorar la performance de foldl grandes.

Implementación

foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)

foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs

Chapter XI: Higher-Order Functions

Haskell is a functional programming language: that means that the main way in which we compute things is by defining functions which describe how to transform the inputs into the required output. Haskell is also functional in a more distinctive way: functions are data in Haskell, and can be treated just like data of any other type.

Una función de alto orden es una función que toma una función como parámetro o retorna una función como resultado.

Operadores $ y .

El operador . nos permite realizar composición de funciones con la misma semántica que en matemática:

(.) :: (b->c) -> (a->b) -> (a->c)

El operador . asocia a la derecha: f . g . h = f . (g . h)

El operador de aplicación $ nos permite aplicar un argumento sobre una función:

($) :: (a->b) -> a -> b

Por ejemplo, f $ x = (f x). El operador se utiliza para omitir paréntesis en funciones como f (g (h x)) = f $ g \$ h x También sirve cuando necesitamos que la aplicación en si sea una función. Por ejemplo: zipWith ($) [sum,product] [ [1,2],[3,4] ] nos permite aplicar las funciones que se encuentran en la primera lista sobre los elementos de la segunda.

Abstracciones lambda

Haskell nos permite escribir funciones que no tienen un nombre asociado. A esto se les llama expresiones lambda. Por ejemplo: \x -> x+1 es la función que suma 1.

Estas funciones también sirven cuando no podemos definir una función de forma independiente:

mapFun fs x = map (\f -> f x) fs

Notar que x no es parte de los argumentos de la función, pero si es parte de la definición. La única forma de replicar esto sin utilizar lambdas es con definiciones locales:

mapFun fs x = map FOO fs
  where FOO f = f x

Las funciones lambda pueden tomar varias entradas. Por ejemplo: comp2 f g = (\x y -> g (f x) (f y))

Partial Application

any function taking two or more arguments can be partially applied to one or more arguments. This gives a powerful way of forming functions as results.

por ejemplo: doubleAll = map (multiply 2) retorna una función que tiene como entrada una lista y devuelve esta lista duplicada. Se retorna una función por application parcial de map, ya que faltaba el argumento de la lista. A su vez, también se aplica aplicación parcial sobre la función multiply. Ya que se deja fijo un argumento, se retorna una función de tipo Int->Int.

Sin embargo, no siempre se puede realizar aplicación parcial de forma directa, esto es porque el argumento que queremos aplicarle la función no siempre es el primero. Esto se soluciona fácilmente con una función lambda. Ejemplo: partial = (\x -> notPartial x 2)

Operator Sections.

Los operadores se pueden aplicar parcialmente de ambos lados, a eso se le conoce como operator sections. Los mismos siguen esta regla:

(op x) y = y op x
(x op) y = x op y

Ejemplos de esto:

(+2) = (\x -> x+2)
(>2) = (\x -> x>2)
(3:) = (\xs -> 3:xs)
($ 3) = (\f -> f $ 3)

Curried functions

Partial application can appear confusing: in some contexts, functions appear to take one argument, and in others more than one. In fact, every function in Haskell takes exactly one argument.

En efecto, la firma a -> b -> c -> d es la simplificación de a -> (b-> (c->d)) . Esto se da porque el operador -> es right associative.

Observar que la flecha -> no es asociativa. Por ejemplo, f (a->a)->b \(\neq\) f a->a->b. La primera función espera como argumento una función de a a a y retorna b mientras que la segunda espera dos argumentos de tipo a.

Rule of cancellation

Para determinar el type de una función aplicamos la regla de la cancelación:

Dada una función t1->t2->...->tn->t y sus argumentos aplicados e1::t1,e2::t2,...,ek::tk. Suponiendo $k<n$ el resultado se da **cancelando** los tipos desde \([1\dots k \) : tk+1 -> tk+2 -> ... -> tn -> t

Currying and uncurrying

Existen dos formas de modelar funciones. La forma uncurried se basa en mandar todos los argumentos como una tuple. Por ejemplo:

(*uc) :: (Integer,Integer) -> Integer
(*uc) (x,y) = x*y

Mientras que la version curryficada es:

( * ) Integer -> Integer -> Integer
( * ) x y = x * y

La forma curryficada tiene dos ventajas: Notación más legible y permite partial application. Es posible pasar de notación curry a uncurry sin dificultades. Las funciones curry y uncurry del Prelude permiten esta transformación.

curry :: ((a,b)->c) -> (a->b->c)
curry f x y = f (x,y)

uncurry :: (a->b->c) -> ((a,b)->c)
uncurry f (x,y) = f x y

Datatype Constructors

¡Los constructores de datatypes también son funciones! Pueden aplicarse parcialmente, pasarse como argumentos y retornados como resultados. El siguiente ejemplo crea una lista de personas utilizando listas: zipWith Person ["GeraInt","Bob"] [22,23]

Verification & General functions

Principle of extensionality

Two functions f and g are equal if they have the same value at every argument.

This is called extensionality in contrast to the idea of intentionality in which we say two functions are the same only if they have the same definitions – we no longer think of them as black boxes; we are allowed to look inside them to see how the mechanisms work, as it were.

Esto quiere decir, para probar que dos funciones son iguales utilizo su definición para probar que ambas tienen el mismo resultado para todo argumento.

NOTA: No podemos utilizar QuickCheck de forma convencional para funciones de alto orden. Podemos pasarle una función de ejemplo, o probar con una instancia de su signature con funciones concretas.

Chapter XII: Developing Higher order Programs

A combinator is a function, typically of higher order. Its etymology comes from the \(\lambda\) calculus.

How can the program be designed? We focus on the data structures which the program will produce, and we can see the program as working by making a series of modifications to the data with which we begin.

La filosofa de diseño data-driven es una práctica común en la programación funcional.

Chapter XIII: Overloading, type classes & type checking

Overloading

Why should we overload?

1. Reuse: Se puede reutilizar la función sobre muchos tipos distintos.
2. Readability: Es más legible tener una única función con un significado semántico claro que varias para cada caso.

Overloading nos permite tener un == global:

(==) :: Char -> Bool
(==) :: [Char] -> Bool

Classes

We call the collection of types over which a function is defined a type class or simply a class.

Los tipos que pueden ser equiparados son los que forman parte de la clase Eq.

La definición de una clase es la siguiente:

class Name ty where
    ... signature involving type variable ty ...

Por ejemplo:

class Eq a where
  (==) :: a->a->Bool

Los miembros de un type class se le llaman sus instancias. Y un tipo es una instancia de una clase si se proporciona una implementación de la interfaz para ese tipo.

¿Como exigimos que los tipos de una función pertenezcan a una clase? Tenemos que exigir un context. En la signature, por ejemplo:

allEqual :: Eq a => a->a->a->Bool

Instances

Para definir una instancia de un tipo debemos implementar su interface:

instance Eq Bool where
  True == True = True
  False == False = True
  _ == _ = False 

A su vez, a una instancia se le puede exigir un contexto. Por ejemplo

instance Info a => Info [a] where ...

De esta manera exigimos que el tipo adentro de la lista también sea instancia de Info.

Limitaciones

Las instancias en Haskell son globales, no son locales a un módulo. También hay limitaciones sobre lo que puede ser una instancia. El tipo de una instancia puede ser un tipo base, una lista, 2-úplas o un constructor tipo shape. Se puede flexibilizar este control, desactivando este estándar de Haskell 2010 mediante la bandera de GHC: {-# OPTIONS GHC -XFlexibleInstances #-}

Default definitions

A una clase se le pueden dar definiciones por default, estas pueden ser overridden en la declaración de una instancia.

class Eq a where
(==),(/=) :: a->a->Bool 
x /= y = not (x==y)
x == y = not (x/=y)

Derivaciones

A su vez, una clase o instancia puede depender que los tipos con que trabaja pertenezcan a otras clases. Por ejemplo, una instancia de Ord también debe estar en Eq. Para reflejar esto:

class Eq a => Ord a where
 (<), (<=), (>), (>=) :: a->a->Bool
 max,min :: a->a->a
 compare :: a->a->Ordering

Podemos entender que la clase Ord hereda las operaciones de la clase Eq!

Multiple constraints

Para indiciar que un tipo debe pertenecer a varias clases:

vSort :: (Ord a, Show a) => [a] ->String

instance (Eq a, Eq b) => Eq (a,b) where
(x,y) == (z,w) = x==z && y==w

class (Ord a, show a) => OrdShow a

Esto puede verse como multiple inheritance.

Haskell Classes

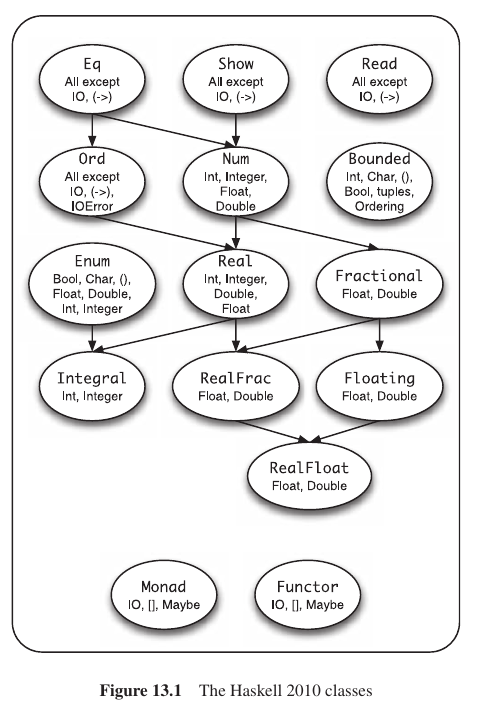
1. Eq: Exige las operaciones == y /=
2. Ord: Exige los operadores de comparación, min y max.
3. Enum: Funciones de sucesor y predecesor, fromEnum toEnum, etc.
4. Bounded: Existe dos números cotas max y min.
5. Show: Implementa la función show para poder transformar el obj a string.
6. Read: Parses un string para obtener el obj.

La clase base de todos los números es Num. La cual exige los operadores +,-,*, la negación, valor absoluto, sucesor, y transformar desde entero a dicho tipo.

Los integer pertenecen a la clase integral la cual tiene las funciones quot,rem y div,mod.

La clase Fractional sirve para representar números Racionales. Exige el operador de división, el inverso, etc.

Derivar instancias

Para evitar tener que escribir instance triviales. Tenemos la syntactic sugar de deriving, la cual nos permite declarar de que clase es un tipo, utilizando las operaciones default de este. Nonetheless, podemos cambiar las operaciones default por las nuestras:

data People = Person Name Age
  deriving (Eq,Show)

Una diferencia notable entre Haskell y lenguajes orientados a objetos como Java es que el primero no tiene dynamic binding, es decir. Si bien existen tipos polimórficos, una instancia de un objeto es de un tipo en concreto. Por ejemplo, una lista es homogénea en ese sentido.

Type Declarations

¿Por que declarar el tipo de una función?

1. The type of an object is the most important single piece of documentation for the object, since it tells us how it can be used – what arguments need to be passed to it, and what type the result has – without us having to understand precisely how it is implemented.

2. Nos permite dar un tipo más específico a una función.

3. Nos permite detectar errores al definir una función.

Type Checking

Al chequear una función se debe verificar que:

1. Las guardas, si hay, son de tipo Bool.
2. Los valores de las expresiones coinciden con el valor de retorno
3. Los patrones son consistentes con los argumentos.

Se dice que un patrón es consistente si matches (algún) elemento del tipo.

Chapter XIV: Algebraic Types

Los tipos algebraicos ya vistos son la suma (data Type = A | B) y el producto (data Type = A B). Se dice que este tipo de datos es algebraico porque el Data Type está compuesto mediante operaciones algebraicas.

Adicionalmente los tipos de datos algebraicos pueden ser recursivos:

data NTree = NilT | Node Integer NTree NTree

Finalmente, el nombre del tipo de dato puede estar seguido de variables en el lado derecho de la igualdad, volviéndolo polimórfico. Por ejemplo, el tipo de dato Maybe utilizado para modelar errores:

data Maybe a = Nothing | Just a

Notar que los enumerados son constructores sin argumentos, los tipos productos tienen un solo constructor y los de suma tienen varios constructores con múltiples argumentos.

Las definiciones sobre datos algebraicos usan pattern matching para distinguir entre las distintas alternativas.

Es posible derivar instancias de clases de tipos algebraicos utilizando la syntactic sugar deriving:

data Season = Spring | Summer | Autumn | Winter 
  deriving(Eq,Ord,Enum,Show,Read)

Para los tipos recursivos, la recursión primitiva es un mecanismo seguro para implementar funciones sobre los mismos.

Constructores infijos

Se puede expresar los constructores mediante notación infija rodeándolos del carácter ":". Por ejemplo:

data Expr = Lit Integer |
            Expr :+: Expr |
            Expr :-: Expr

Se le llama a un conjunto de funciones mutually recursive si realizan varias llamadas recursivas entre ellas.

Polymorphic

Los tipos algebraicos pueden tener variables para volverlos polimórficos: data Paris a = Pr a a Instancias de lo anterior son:

Pr 2 3 :: Paris Integer
Pr [] [3] :: Paris [Integer]

Podemos definir funciones polimórficas sobre estos tipos:

equalPair :: Eq a => Pairs a -> Bool
equalPair (Pr x y) = x==y

Dado que las definiciones pueden tener ms de un parámetro:

data Either a b = Left a | Right b
  deriving (Eq,Ord,Read,Show)
Left "Duke of" :: Either String Int
Right 3312 :: Either String Int

isLeft :: Either a b -> Bool
isLeft (Left _) = True
isRight (Right _) = False

Modelling program errors

El problema de la función error es que toda computación útil que se haya realizado se pierde. Existen dos approaches para resolver este problema

Dummy values

Para toda función f podemos envolverla para que devuelva un aviso de error dado una condición:

fErr y x
  | cond = y
    otherwise = f x

Error Types

Why not instead return an error value as a result?

data Maybe a = Nothing | Just a
  deriving (Eq,Ord,Read,Show)

De esta manera podemos definir:

fErr x 
  | cond = Nothing --There was an error.
  | otherwise = Just (f x)

El tipo Maybe nos permite levantar una excepción. Cuando se da una excepción podemos:

1. Trasmitir el error a traves de la función (mapMaybe) mapMaybe g Nothing = Nothing mapMaybe g (Just x) = Just (g x)
2. Atrapar el error (maybe) maybe n f Nothing = n maybe n f (Just x) = f x

Chapter XV: Huffman codes

Modules

In the definition of Haskell 2010, there is no identification between modules and files. Nonetheless, we choose here to write one module per file, and indeed this is required by GHC.

Para importar un módulo desde un archivo:

module Bee where

import Ant

Por defecto se exportan todas las definiciones de un módulo y se exportan todas las del mismo.

Para controlar lo que el módulo exporta podemos controlarlo mediante la declarativa module: module Bee (beeKeeper, Ants (..), anteater) where .... Esto hace que únicamente se exporte las funciones beekeeper, anteater, y el data Ants con sus constructores. Si se omite "(..)" no se importan los constructores generando un tipo de dato abstracto.

Observar que para decir que todas las definiciones de un módulo deben ser exportadas escribimos module M. Por ejemplo:

module Bee (module Bee, module Ant) where

Notar que todo sistema compilado requiere un módulo Main. Un archivo sin declaración de module se supone que tiene como header module Main(main) where

En vez de decir lo que necesitamos de un módulo, podemos declarar lo que no necesitamos. Por ejemplo: import Ant hiding (anteater)

Para evitar que dos funciones con el mismo nombre tengan conflicto, podemos utilizar el qualified name de un módulo. De forma de que las funciones de un módulo se invocan mediante moduleName.foo . Para esto especificamos: import qualified moduleName. Si no se importa un módulo qualified se pueden utilizar ambas formas para mencionar una función (module.foo or foo).

Modular design

Las características de un módulo son bastante similares a la que debe tener una clase o un archivo de C:

1. Cada módulo tiene un claro rol identificable.
2. Cada módulo hace una sola tarea.
3. Un módulo debe hacer una cosa, pero hacerla completamente. Debe ser autocontenido.
4. Cada módulo debe exportar únicamente lo necesario (i.e su interfaz). Esto sigue el principio de information-hiding.
5. Los módulos deben ser pequeños. No más de una página de código.

Chapter XVI: Abstract data types

En esencia. Los tipos abstractos de datos son módulos donde se ocultan los constructores y se da un set de operaciones los cuales me permiten operar sobre estructuras de datos genéricas.

ADT nos permite ocultar la información, encapsular comportamiento y reutilizar código a través de polimorfismo.

Los tipos abstractos de datos (TAD) tienen 3 propiedades importantes:

1. Son una representación natural de una estructura, avoids being over-specific.
2. The signature of the data type is a firm interface between the user and the implementer. The dev of both systems can proceed independently
3. If the implementation of a type changes, there should be no change in the programs that use such datatype.

Chapter XVII: Lazy Programming

El método de evaluación perezosa de Haskell nos permite definir expresiones y estructuras de datos sin tener que construirlas completamente. Esto provee un estilo de programación único y permite aplicar nuevas técnicas de programación.

El funcionamiento de lazy evaluation es el siguiente:

1. arguments to functions are evaluated only when this is necessary for evaluation to continue;
2. an argument is not necessarily evaluated fully: only the parts that are needed are examined;
3. an argument is evaluated at most only once. This is done in the implementation by replacing expressions by graphs and calculating over them.

A su vez en las definiciones con guardas y funciones locales, se aplica la definición únicamente si es necesaria. Para las condiciones de las guardas se verifica el pattern matching que coincida, luego se procede a evaluar las condiciones hasta que se llegue a una que de True. Una vez que se llega a una condición verdadera se remplaza simbólicamente la definición, no se continúa evaluando condiciones.

Los operadores utilizan evaluación de circuito cerrado. Por ejemplo, el operador and && si el operando izquierdo da False entonces no se evalúa el operando derecho. Esto se cumple de forma análoga para el or ||.

Evaluation Order

Otra característica de Haskell es el orden en que se evalúan las funciones:

La sustitución se aplica de afuera para adentro. Por ejemplo: f 30 (- 20 20) -> 30+(-20 20)+(-20 20). Luego, la evaluación es de izquierda a derecha: (+ 1 1) + (+ 2 2) = 2 + (+ 2 2)

List comprehensions

A list comprehension tiene la forma [e | q1 , ... , qk ] donde cada q puede ser un generador p <- lExp donde p es un patrón y lExp es una expresión que tiene como resultado una lista. La otra opción es que q sea un test, es decir una expresión booleana.

Las list comprehension con múltiples generadores dan como resultado la combinación de los elementos de cada generador. Por ejemplo [(x,y) | x<-[1,2] y<-[4,5]] ---> [(1,4) (1,5) (2,4) (2,5)]. Es importante destacar como se procesa las funciones con múltiples generadores, ya que nos podemos basar en el primer generador para definir los generadores que van después. Esto se debe a que el generador actúa como una suerte de for anidado. Por ejemplo: triangle n = [ (x,y) | x <- [1 .. n] , y <- [1 .. x] ].

Un ejemplo del uso de esta técnica es para armar listas de permutaciones:

perms :: Eq a => [a] -> [[a]]
perms [] = [[]]
perms xs = [x:ps | x<-xs, ps<-(xs\\[x])]

El operador xs\\ys definido en Data.List nos retorna la diferencia entre xs e ys , donde se remueve cada elemento que se encuentra en ys en xs, teniendo en cuenta multiplicidades.

Ejemplo del producto entre dos matrices:

matrixProduct :: Matrix -> Matrix -> Matrix
matrixProduct m p = [ [scalarProduct r c | c <- columns p] | r <- m ]
  where columns y = [ [ z!!j | z <- y ] | j <- [0 .. s] ]
    where s = length (head y)-1

Se dice que un patrón es refutable si el elemento que se tiene no encaja con el patrón que se solicita.

Data directed programming

This is an approach where we design the program by thinking about it as a sequence of transformations of data. In a traditional language it may well be too inefficient to do this in practice, as we might have to compute a series of complex data structures which are ‘internal’ to the program. In a lazy language these are only constructed as they are needed, and in practice they may never be constructed completely: we just build a data structure incrementally, and once a part of it has been used, it can be ‘recycled’. Luckily this is done by the implementation, and we do not have to worry about it ourselves.

Por ejemplo, observar el siguiente comportamiento:

sumFourthPowers n = sum (map (^4) [1 .. n])

sumFourthPowers n -> sum (map (^4) [1 .. n]) ->  sum (map (^4) (1:[2 .. n])) -> sum (1^4 : map (^4) [2 .. n]) -> (1^4) + sum (map (^4) [2 .. n]) -> 1 + sum (map (^4) [2 .. n]) ...

Observar que nunca se construye la lista intermedia, a medida que se obtiene un ítem de la lista, ya se hacen los cálculos. Por lo tanto, no resulta ineficiente tener esta definición de lista.

Un ejemplo muy interesante es el de hallar el mínimo de una lista. ¡En Haskell lo más eficiente es ordenarla y luego tomar el head! Esto es porque la operación de ordenar el primer paso que hace es obtener el elemento más grande y colocarlo al frente de la lista. Al hacer esto, haskell no continúa generando el resultado, sino que ya enseguida devuelve el ítem. ¡Por lo que la lista nunca se llega a ordenar!

Infinite Lists

¡Como Haskell construye parcialmente una estructura de datos, es posible trabajar con estructuras infinitas! Por ejemplo: las sumas parciales sobre una lista infinita son calculables:

ones = 1: ones
addFirstTwo (x:y:xs)= x+y
addFirstTwo ones = 2

La función iterate nos permite generar una lista a partir de una función y un valor inicial. Por ejemplo: iterate (+2) 0 = [0,2,4,6,7,...].

Ejemplos elegantes del uso de listas infinitas es el de la generación de números primos:

primes  = sieve [2 .. ]
sieve (x:xs) = x : sieve [ y | y <- xs , y ‘mod‘ x > 0]

Básicamente se va generando una lista donde cada vez se tienen que cumplir que los elementos que ya están en la lista, si se les hace el mod, tiene que dar 0.

Es importante destacar que si nos preguntamos si un numero está en esta lista, hay una respuesta. ¿Pero cómo probamos que no hay? ¡No hay forma! ya que la lista es infinita. Para solucionar esto, se puede aplicar la propiedad de que la lista generada está en orden para parar en la raíz cuadrada del número.

Otro ejemplo es un pseudo-generador de números aleatorios:

nextRand :: Integer -> Integer
nextRand n = (multiplier*n + increment) ‘mod‘ modulus
randomSequence :: Integer -> [Integer]
randomSequence = iterate nextRand

Why infinite lists?

¿Por qué las listas infinitas son ventajosas en la programación funcional?

Primero, las listas son una versión más abstracta de un programa. Son más simples y elegantes de escribir. Nos olvidamos del tamaño de las estructuras, no hay que alocar recursos para algo, sino que se va generando sobre la marcha.

Por otro lado, las listas infinitas separan la generación de los datos de su transformación. Permite la modularization.

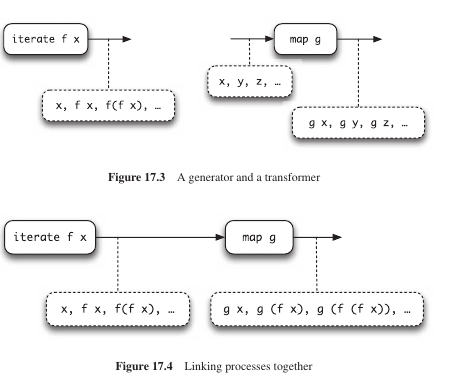
Las listas infinitas combinadas con transformaciones recursivas son una poderosa herramienta de la programación funcional.

Proofs

Es posible hacer demostraciones sobre listas infinitas. Para ello se recurre a la noción de resultados parciales y listas indefinidas. Una lista indefinida es aquella que su computación es indeterminada:

undef :: a 
undef = undef

Una lista infinita puede entenderse como una lista con infinitas listas parciales:

n = [1 ..] - > 1: [2 ..] , 1: 2 [3 ...], 1:2:3:[4, ..], 1:2:3:4:[5 ..]

Con estas definiciones podemos probar cosas sobre las listas parciales. Y aplicar inducción. Es decir, probar una propiedad P(xs) para todas las listas finitas y parciales tenemos que probar:

• Base cases: Prove P([]) and P(undef).
• Induction step: Prove P(x:xs) assuming that P(xs) holds already.

Es importante destacar la técnica de "lists of successes" donde se interpreta el contenido de una lista como las respuestas de una función y la lista vacía cuando no hay respuesta.

In giving an infinite list of prime or random numbers we provide an unlimited resource: we do not have to know how much of the resource we need while constructing the program; this abstraction makes programming simpler and clearer.

Infinite lists provide a mechanism for process-based programming in a functional setting.

Notas Fing

El modelo de computación de programación funcional es por reducción. Esto significa que las funciones actúan como reglas de cómputo. En cada paso de la evaluación de una expresión se debe deducir que subexpresión reducir.

Se le llama redex a expresiones formadas por una función aplicada a argumentos la cual es posible reducirla.

Dado que una expresión puede tener muchos redex, surge la pregunta de cuál se debe evaluar primero. Así surgiendo las estrategias de evaluación.

Ejemplo de estas estrategias son leftmost innermost la cual reduce los redex más internos y más a la izquierda. El leftmost outermost reduce el redex más externo y más a la izquierda:

Leftmost innermost: $square (1+2) -> square (3) -> 3x3 -> 9$.

Leftmost outermost: $square(1+2) -> (1+2)x(1+2) -> 3x(1+2) -> 3x3 -> 9$

Undefined

El valor indefinido, usualmente notado como ⊥ (bottom), denota tanto la no terminación como la terminación anormal de un programa. Podemos pensar que todos los tipos tienen un valor ⊥.

Call by value & Call by name

Call by value refiere a que cuando se evalúa una expresión los argumentos se pasan por valor. Mientras que by name se pasa la expresión que lo genera. Ejemplo claro:

f x = 78x+4
g x = (x,x+1)

Call by value:
g (f 1) -> g (78*1+4) -> g(82) -> (82,82+1) -> (82,83)
Call by name:
g (f 1) -> g (f 1) -> (f 1,(f 1)+1) -> (82,82+1) -> 83

En haskell, se utiliza un grafo de expresiones donde hay punteros que apuntan a mismos lugares donde ocurre una expresión, de esta manera un argumento será copiado una sola vez. El uso de call by name junto a esta forma de sharing se le conoce como lazy-evaluation o call-by-need.

Funciones estrictas

Se dice que una función es estricta si cumple que: \(f ⊥ = ⊥\) . De lo contrario, se le llama no estricta.

¡En call by value todas las funciones son estrictas, pero en call by name no!

Lazy Evaluation

Propiedad: Con lazy evaluation toda expresión se evalúa hasta lo que le requiera el contexto en que se encuentra

Por lo tanto, las estructuras infinitas pueden entenderse más bien como estructuras potencialmente infinitas. Así permitiendo locuras como:

ones = 1 : ones
take 5 ones = [1,1,1,1,1]

Mónadas

Una monada es una interfaz de programación que permite simular la concatenación de efectos computacionales en un lenguaje funcional como Haskell. También es una sintaxis que permite simplificar procesos repetitivos de código modelando el comportamiento del programa embebiendo los operadores >>= y return. Ejemplos de monadas en el Prelude son IO, Maybe y []

En esencia, una clase Monad es aquella que implementa las siguientes funciones:

class Monad m where
    (>>=) :: m a -> (a -> m b) -> m b
    (>>) :: m a -> m b -> m b -- opcional
    return :: a -> m a
    fail :: String -> m a --opcional
    m >> k = m >>= \_ -> k --default implementation

Donde estas funciones deben cumplir las siguientes propiedades:

return a>>=k = k a
m >>= return = m
m >>= (\x -> k x >>= h) = (m >>= k) >>= h

Las operaciones de bind (>> y >>=) combinan dos valores monádicos mientras que el return inyecta un valor en una mónada. El resultado del bind >>= es el de combinar ma y mb en un valor monadico. El bind >> se usa cuando no nos interesa el resultado de la mónada a.

The precise meaning of binding depends, of course, on the monad. For example, in the IO monad, x >>= y performs two actions sequentially, passing the result of the first into the second.

Para trabajar con mónadas, muchas se trabajan en su versión con azúcar sintáctica. La notación do se basa en las siguientes reglas:

do e1 ; e2 = e1 >> e2 do p <- e1 ; e2 = e1 >>= (\p -> e2)

En el caso de que una mónada pueda "fallar" las reglas de do son:

do p <- e1 ; e2 = e1 >>= (\v -> case v of p-> e2; _->fail "s")

Existe una clase especial llamada MonadPlus la cual se utiliza cuando la mónada tiene un zero element y una plus operation.

class (Monad m) => MonadPlus m where
    mzero :: m a
    mplus :: m a  -> m a -> m a 

Donde:
m >>= (\x -> mzero) = mzero
mzero >> m = mzero

m `mplus` mzero = m
mzero `mplus` m = m

La Recordar que un bloque de do-notation debe seguir indentación correcta (todos los componenetes al mismo nivel).

Ahora veamos que podemos hacer con esto...

IO Monad (Review)

La IO monad nos permite operar sobre la entrada y salida. Algunas de las mejores funciones son:

getLine :: IO String
getChar :: IO Char 
putChar :: Char -> IO ()
putStr :: String -> IO ()
putStrLn :: String -> IO()

Y para el manejo de archivos:

type FilePath = String
readFile :: FilePath → IO String
writeFile :: FilePath → String → IO ()
appendFile :: FilePath → String → IO ()

Así como colado, podemos imprimir una variable con la función print :: Show a => a -> IO ()

Monad IORef

La mónada Data.IORef

newIORef :: a -> IO (IORef a)
readIORef :: IORef a -> IO a
writeIOReff :: IORef a -> a -> IO ()
modifyIORef :: IORef a -> (a -> a) -> IO()

Esta monada permite mantener el estado de una referencia. Leer/Escribir en esta. Lo más parecido a una variable en programación imperativa.

Ejemplo:

main = do v <- newIORef 10
          modifyIORef v (+5)
          x <- readIORef v
          print x

writeIORef :: IORef a -> a -> IO () Sobrescribe una referencia. modifyIORef :: IORef a -> (a -> a) -> IO () Aplica f sobre una referencia. readIORef :: IORef a -> IO a : lee una referencia, la guarda en la mónada IO.

Monad LiftM2

La mónada LiftM2 sirve para llevar datos puros de haskell a una mónada (particularmente 2 datos). Por ejemplo:

lift M2 :: Monad m => (a -> b -> c) -> m a -> m b -> m c lift M2 f m m2 = do x <- m y <- m2 return (f x y)

Podría usarse en: eval (Add x y) = liftM2 (+) (eval x) (eval y)

List Monad

(>>=) :: [a] -> (a -> [b]) -> [b]
(>>=) l f = concatMap f l 
return :: [a]
return x = [x]

Donde concatMap :: Foldable t => (a -> [b]) -> t a -> [b]
Mapea una función sobre todos los elementos del input y concatena los resultados de los elementos en una sola lista.

What monads really provide is modularity. That is, by defining an operation monadically, we can hide underlying machinery in a way that allows new features to be incorporated into the monad transparently.

State Monad

¿Como transportamos un estado?

Veamos el ejemplo de llevar un estado para la recorrida de un arbol binario. La forma de hacer esto sin utilizar mónadas es:

numTree (Fork l r) = (\cont -> let (l2,cont2) = numTree l cont; (r3,cont3)= numTree r cont2 in (Fork l2 r3 cont3)

Control.Monad.State implementa una mónada de estado que hace esto más conveniente:

numTree :: Tree a -> State Int (Tree (Int,a))
numTree (Leaf a) = do   cont <- get
                        put (cont+1)
                        return (Leaf (cont,a))
numTree (Fork l r) = do l2 <- numTree l
                        r2 <- numTree r
                        return (Fork l2 r2)

Wow! El estado se mueve implícitamente en la mónada. Veamos cómo se implementa este mecanismo estudiando las definiciones de >>= y return:

type State s a = s -> (a,s)

return a = (\s -> (a,s))
(>>=) m f = (\s -> let (a,s2) = m s in f a s2)

Por lo que: numTree (Fork l r) = numTree l >>= (\a -> numTree r s) >>= (\b -> (\s -> (Fork a b, s))

get = (\s -> (s,s))
put s = (\_ -> ((),s))

Ejecutamos una mónada state con la función runState :: State s a -> s -> (a,s). La cual dada una mónada y un estado inicial retorna una tuple (estado final, resultado)

Maybe Monad

En el fondo lo que estamos es resolviendo el problema de escribir código repetitivo... no podemos abstraer este código en algunas operaciones/abstracciones para que pase "tras bambalinas" en el trabajo relevante de una función.

return = Just m >>= f = case m of Nothing -> Nothing Just x -> f x eval (Add x y) = eval x >>= (\a -> eval y >>= (\b -> return (a+b))) eval (Neg x) = eval x >>= (\a -> return (-1*a))

Tomo un maybe y una función que va a utilizar el valor de la mónada... (¡Explicación del bind!)

En el fondo las lambda functions son los que transportan el efecto computacional de la mónada...

La clave de esta mónada es que si una computación da Nothing entonces el resultado de las demás computaciones es Nothing too. Por ejemplo m1 = do x<- Just 3; y <- Nothing; ¡return x retorna Nothing a pesar de que el resultado de lo que se va a retornar dio bien!

Reader (Environment) Monad

Control.Monad.Reader nos sirve para realzar computaciones que leen valores de un ambiente compartido.

data Reader e a = Reader (e -> a)
runReader (Reader r) = r

instance Monad (Reader e) where
    return a = Reader $ (\e->a) 
    (Reader r) >>= f = Reader $ (\e -> runReader (f (r e)))

    ask :: Reader e e 
    ask = Reader id

    local :: (e->e) -> reader e a - > Reader e a 
    local f c = Reader $ (\e -> runReadedr c (f e))

The Reader monad (also called the Environment monad). Represents a computation, which can read values from a shared environment, pass values from function to function, and execute sub-computations in a modified environment. Using Reader monad for such computations is often clearer and easier than using the State monad.

La función ask sirve para obtener el environment de la mónada ask :: Reader env env. runReader :: Reader env a -> env -> a Permite leer un reader, con un ambiente inicial definido en env.

Local permite modificar el ambiente local :: (r->r) -> m a -> m a. Donde r->r es la funcion que modifica el ambiente y el primer m a el reader que corre en el ambiente. Este local ejecuta una computación en este ambiente modificado.

Any time you have a "constant" in a computation that you need at various points, but really you would like to be able to perform the same computation with different values, then you should use a reader monad.

Annotations:

The dot operator

Es el operador de composición. Por lo tanto:

g(x) = f(h(z(x)))

es equivalente a escribir en haskell:

g = f . h . z g x = f ( h (z x))

Operators

Los operadores se definen escribiéndolos entre paréntesis: (!@#) int -> int -> int (!@#) x y = 2

¡Esto también sirve para escribirlos con notación prefija! Recordar que la notación infija se puede utilizar haciendo: 2 'f' 2

it keyword

La palabra it conserva el resultado de la última operación. Por lo tanto: 2+2 it+2 it*2 it imprime al final 12

QuickCheck operator ==>

El operador ==> funciona como un implica para verificar una propiedad. Modo de uso:

prop :: Integer -> Integer -> Property
prop a b =
  (b /= 0) ==> a*((-b) `div` a)+b==0

Esto hace que la propiedad también se cumpla cuando b==0, ya que no se debe probar el consecuente del implica.

dbp1 :: Database -> BarCode -> Name -> Price -> Property dbp1 db bc n p = ((look db bc)==("Unknown Item",0)) ==> (length (remCode bc (newCode bc n p db))) == (length db)\

Re-implementaciones + QuickCheck

QuickCheck es muy práctico para probar que el comportamiento de una función que debe ser igual a otra efectivamente lo es. Basta con definir la propiedad:

prop :: f -> f -> p -> Bool
prop f1 f2 p = f1 p == f2 p

The @

El @ nos permite generar un alias. Se puede leer x@y como "x as y". Un ejemplo de uso: [x | x@(a,b)<-xs,a>0]

Funciones memorables

sequence :: Monad m => [m a] -> m [a] : Evalúa cada acción de la sequencia de izquierda a derecha, retornando los resultados en una mónada con la lista.

repeat :: a -> [a] : Retorna la lista infinita del elemento que se dio como entrada.

elem (Foldable t, Eq a) => a -> t a -> Bool : Busca un elemento x en una lista xs, retorna True o False.

const :: a -> b -> a : const x y = x para todo par (x,y).

null :: Foldable t => t a -> Bool : Re torna true si la lista está vacía.

all :: Foldable t => (a -> Bool) -> t a -> Bool : Retorna true si todos los elementos de la lista satisfacen el predicado.

curry :: ((a, b) -> c) -> a -> b -> c : Dada una función f (x,y), la currifica: f x y.

uncurry :: (a->b->c) -> (a,b) -> c : Uncurrifica una función f x y: f (x,y)

Apuntes Programación Funcional Verano 2022

Clase TiposDef.mp4

Un programa en PF consiste esencialmente de una lista de definiciones (funciones). Estas se escriben como ecuaciones , eventualmente con una descripción de tipo (signature)

Ej: num::Integer num = 3 + 6

Obs: La signature es omisible ya que esta se puede inferir. Sin embargo, es recomendable utilizar la signature ya que forma parte de la documentación del programa.

Para definir funciones, especificamos sus parámetros funcionales:

square :: Integer -> Integer
square x = x*x

Las funciones se cargan en el intérprete y luego pueden ser ejecutadas:

ghcl file.hs
f (suponiendo que file.hs contiene la definición de f)

Los argumentos de una funcion se escriben con un espacio para ejecutarse: "f 1 2 3"

Los tipos forman parte de la especificación del sistema, el tipado es esencial para la construcción de software confiable.

El tipo de las expresiones de haskell nos cuenta mucho sobre su funcionamiento!

El tipado en haskell es fuerte: Toda expresión debe tener un tipo. Toda constante, variable, operador y función debe tener un tipo.

El chequeo de los tipos en haskell es estático: Se chequea en compilation time

Haskell nos asegura type safety: Al ejecutar, los programas nunca van a errores de tipos.

Well-typed programs never "go wrong"

Tipos basicos de Haskell

• Bool: Boolean. Sus constantes son "True" y "False"
• Char
• String
• Int (entero acotado)
• Integer (entero no acotado)
• Float
• Double

Obs: Los types siempre tienen mayúscula.

Boolean

Los booleanos tienen las primitivas habituales: "not, && y ||" Ejemplo de función booleana:

exOr :: Bool -> Bool -> Bool
exOr x y = (x||y) && not(x&&y)

Una forma alternativa de definir funciones es utilizando la técnica de pattern matching

exOr:: Bool->Bool->Bool
exOr True y = not y
exOr False y = y

Integers

Existen dos tipos de enteros: Int e Integer (no acotado). Tenemos los operadores habituales: +,-,*,^,div,mod,abs,negate. (Observar que los operadores están sobrecargados)

Los enteros pueden ser comparados por operadores relacionales: <,>,>=,==,/=,...

Ejemplo: min :: Integer -> Integer -> Integer min x y = if x<= y then x else y

La conversión de Int a Integer no es explicita y debe ser utilizada al aplicar los operadores primitivos entre Int e Integer:

fromInteger :: Integer -> Int
toInteger :: Int -> Integer

Characters

Los caracteres son codificados por la tabla ASCII. Se escriben entre comillas simples: 'a'. A su vez tenemos los caracteres especiales con el backslash: '\t','\','\n',etc.

La conversión entre carácter y codificación ASCII es a través de:

fromEnum :: Char -> Int
toEnum :: Int -> Char

String

El tipo String se define como una Lista de caracteres. A diferencia de programación imperativa donde los strings son arreglos, aquí se usan listas.

Las constantes de tipo string se escriben entre comillas dobles: "Constante!!1!"

Las funciones show y read permiten convertir entre valores de otros tipos y String:

show(4+3) = "7"
read("3")+4 = 7

Show te da un Stirng para que puedas mostrar, read te deja leer un string para poder interpretarlo.

Reales

Para los reales tenemos Float y Double. Las operaciones aritméticas básicas están disponibles. También tenemos la división real y las trigonométricas.

Existen funciones de conversión para trabajar con Reales y Enteros:

ceiling :: Float->Integer
floor :: Float-> Integer
round :: Float -> Integer

fromInteger :: Integer -> Float
fromIntegral Int -> Float

Clase estructurados.mp4

Además de los tipos básicos, podemos definir tipos estructurados, estos objetos están compuesto por un conjunto de valores.

Tuplas

Una tupla combina en un mismo objeto a un número fijo de valores, cada uno con un tipo determinado (pueden ser distintos).

Es similar un struct de C. A diferencia que los componentes de defininen por un identificador y en las tuplas por la posición.

Ejemplo: Coordenadas cartesianas

(8,23) :: (Int,Int)

El tipo $(t_1,...t_n) consiste en tuplas de valores (v_1,...,v_n) :: (t_1,...,t_n).

Para aplicar funciones sobre tuplas se suele usar pattern matching:

nombre :: (String, Int, Int) -> String
nombre (n,e,s) = n

¡Observar que estamos ligando cada elemento de la tupla con un identificador de variable!

Al aplicar la función, los componentes del patrón matchean con los componentes del argumento: ("Pedro",44,1000) -> "Pedro"

También se pueden aplicar wildcards para ignorar componentes y no tener que utilizar identificadores para todos los componentes:

edad (_,e,_) = e
sueldo(_,_,s) = s

Finalmente, se pueden forzar componentes utilizando literales: esPedro("Pedro",,) = True esPedro(,,_) = False

El wildcard completo también puede escribirse como:

esPedro _ = False

Esto hace que se acepte cualquier elemento y retorne false.

Como en el pattern matching se matchean las ecuaciones de arriba para abajo, el tener de nombre Pedro se va a matchear siempre con la primera ecuación.

Sinónimos de Tipos

En haskell le podemos dar nombres a los tipos. Al usar un sinónimo se tiene el mismo efecto de usar el tipo que representa.

Ejemplos:

type Coord = (Int,Int)
distancia: Coord -> Coord -> Float

Listas

Las listas combinan en un mismo objeto a un número q arbitrario de valores, todos de un mismo tipo.

Es decir, a partir del tipo no sé cuántos valores puede contener, lo único que se es el tipo de valores que contiene.

Ejemplos: [8,2,3,1,24] :: [Int] [("Juan",23,1000),("Peter",12,400)] :: [Empleado]

Recordar: Un String es una lista de caracteres:

type String = [Char]

Definición

Definimos inductivamente a las listas de tipo [t] como:

[] - lista vacía
v : vs - lista con al menos 1 elemento donde v in and vs::[t] 

Este operador ":" se le llama cons, toma dos elementos y construye una lista con los objetos definidos a la derecha.

Formas de construir una lista de enteros:

[] [24] 1 : (24 : []) 3 : (1 : (24 : [])) Como cons asocia a la derecha los paréntesis son no redundantes. El compilador soporta sintactic sugar utilizando cons: [1,2,3,4] el compilador lo entiende como 1 : 2 : 3 : 4 : [].

Funciones sobre Listas

Existe una gran cantidad de funciones sobre listas en Prelude. Prelude es la librería que viene incluida por defecto en el compilador de haskell.

Ejemplos: ( ++ (append) ,!!, length, replicate, take ,drop , reverse, etc.)

Las nuevas funciones se definen combinando las funciones anteriores o pattern matching:

dupList xs = xd ++ xs

null [] = True
null(_:_) = False (Composicion con un cons)

head (x : _) = x
tail (_ : xs) = xs

Listas por Comprensión

Notación que permite construir una listea a partir de una descripción de la misma en términos de otra.

A partir de una lista se generan elementos, se testean y transforman para formar los elementos de la lista resultante.

Ejemplo: generación: [x | x <- [1,2,3,4]] ---> [1,2,3,4] testeo: [x | x <- [1,2,3,4], isEven x] ---> [2,4] transformación: [isEven x | x <- [1,2,3,4]] ---> [False,True,False,True]

Donde se liga cada elemento también se puede aplicar pattern matching:
[(x+y) | (x,y) <- [(1,2),(3,4),(4,5)]] ---> [3,7,9]
[(x,y) | x <- [1,2], y <- [3,4]] ---> [(1,3),(1,4),(2,3),(2,4)]

Notar que la lista generada puede ser el parámetro de una función:

evens xs = [x | x<- xd, isEven x]
donde isEven x = mod x 2 == 0

Tipos de Datos Algebraicos

Mediante la definición de tipos de datos algebraicos podemos introducir nuevos tipos

Nos permiten definir, por ejemplo, enumerados:

data PuntoCardinal = Norte | Sur | Este | Oeste
    deriving (Show,Eq)

Observar que se utiliza la palabra reservada data, el nombre y separado con pipes los componentes posibles del tipo. Observar que los componentes llevan mayúsculas, ya que son constantes.

Finalmente, el deriving(Show,¡Eq) es opcional e indica que los valores de PuntoCardinal van a poderse pasar a String con la función show() y pueden compararse con el operador de igualdad (EQ) == != . Si lo anterior no se incluye no vamos a tener estas dos últimas propiedades.

También podemos definir Productos:

data Empleado = Empleado String Int Int
    deriving(Show,Eq)

Al definir un producto escribimos los parámetros que le pasamos al constructor Empleado y a eso decimos que es Data Empleado.

Luego podemos hacer: Empleado "Juan" 25 50000

El pattern matching se aplica a constructores. Ejemplo:

data TEmpleado = CEmpleado String Int Int
    deriving(Show,Eq)
esPedro :: TEmpleado -> Bool
esPedro (CEmpleado "Pedro" _ _) = True
esPedro _			= False

En este ejemplo se observa que estamos matcheando el tipo de dato TEmpleado con aquellos construidos con el constructor CEmpleado, que a su vez el campo nombre es Pedro.

Por último, también podemos expresar con tipos de datos algebraicos ALTERNATIVAS :

data Forma = Circulo Float
        | Rectángulo Float Float
    deriving (Show, Eq)

De esta manera, circulo 2.5 y Rectángulo 4.2 2.2 son dos objetos de un tipo Forma.

En general,

data T = C_1 t_11,...,t1k1
    | C_n t_n1,...,t_nk_n

donde T es el nuevo tipo a introducir y cada \(C_i\) es un constructor de dicho tipo, que toma \(k_i\) parámetros.

Aplicación, Funciones:

area:: Forma -> Float
area (Circulo r) = 3.14 * r*r
area (Rectángulo a b) = b*a

cuadrado l = Rectángulo l l (Observar que esto es una función)

Clase definiciones.mp4

Ecuaciones condicionales

Es posible definir ecuaciones condiciones (como en maths)

abs x | x>=0 = x 
| otherwise = -x

donde otherwise es una condición que siempre es verdadera. Las condiciones se evalúan en secuencia y se toma la primer condición verdadera. Si todas las condiciones son falsas, entonces vamos a tener un error.

Una forma alternativa de construcción de abs x es utilizando un if:

abs x = if x>= 0 then x else -x

Las funciones se pueden definir utilizando pattern matching. De forma infija:

True && b = b
False && _ = False

Los patrones satisfacen la siguiente gramática:

pat ::= _ --wildcard | variable | literal | (pat1,...,patn) --Una tupla | pat:pat --Cons | C pat1 ... patn --C es un constructor | var@pat -- as pattern

Ejemplos:

duplica(x:xs) = x : x : xs
duplica s@(x: xs) = x:s

El s es como decir: (x:xs) AS s. Por lo que al escribir s vamos a estar refiriéndonos al patrón x:s. Esto nos sirve para no desarmar grandes estructuras cuando estamos definiendo una expresión.

Definiciones locales

f x y = (a+1) * (a+2) where a = (x+y)/2

El alcance de dicha definición local es expresión en la parte derecha de la definición de f. Construyo un identificador que luego puedo invocar varias veces para mayor comodidad:

f x y = (a+1)*(b-1) where a = 1212x b= 323x-y

Estas variables locales también las puedo aplicar en ecuaciones condicionales.

Otra forma alternativa es utilizar let/in:

f x y = let a = (x+y)/2 in (a+2)*(a*2)

El alcance de la expresión a es lo que está en la expresión in. Es posible anidar construcciones con let:

let x=2 in let y=x+3 in y*4 Wow!

Operadores

A las funciones definidas en forma infija se les suele llamar operadores. Al escribir un operador entre paréntesis lo convertimos en una función prefija currificada:

(+) 3 4
(*) 7 8
(<) 2 3 -- Esto es equivalente a 2<3

Esto nos sirve para pasar como argumento un operador a funciones:

suma = uncurry (+)
leq = uncurry (<=)

Los operadores infijos deben estar saturados. Esto es que estén presentes todos sus argumentos: 3+3 (OK) pero 3+ (FAIL)

En cambio, al escribir un operador entre paréntesis es posible parametrizarlo parcialmente:

(+) 3 :: Int - > Int (<) 2 : Int - > Bool

Secciones

Las secciones son una sintaxis especial para expresar la parametrización parcial de un operador infijo, se encierra entre paréntesis junto a unos de sus argumentos:

(3+) :: Int - > Int

(3+) 4 ----> 7

Definiciones Anónimas

Es posible definir funciones anonimias (es decir, sin nombre) mediante el uso de las llamadas expresiones lambda.

\lambda x -> x+1

En haskell: \x - > x + 1

La aplicación de una función anónima a sus argumentos se realiza de la misma forma que con las otras funciones:

(\x -> x+1) 2 ----> Genera 3

Las definiciones de funciones con nombre también pueden ser vistas como definiciones en términos de expresiones lambda:

add = \x -> (\y -> x+y)

Clase operacionesListas.mp4

el tipo Lista es uno de las más usadas in Functional Programming. Su relevancia es comparable a los Sets in Mathematics.

A diferencia que en Matemáticas, las listas se definen:

Las listas son un tipo polimórfico (dos constructores): [] :: [a] (constructor nil) (:) :: a -> [a] -> [a] (constructor cons)

Ejemplo cons: 1:(2:(3:[])) -> [1,2,3] ¡El constructor cons asocia a la derecha! Por lo que es equivalente: 1 : 2 : 3 : [].

Tambien existe un sugar syntax, permitiendo escribir directamente: [1,2,3].

Generadores de listas

La expresión [m .. n] denota la lista de valores entre m y n. Por ejemplo [1..4]=[1,2,3,4]. Si m es mayor a n tenemos la lista vacía [].

Divisores de un numero

m 'divide' n = n 'mod' m == 0

Las funciones que toman dos argumentos pueden utilizarse de manera prefija o infija utilizando backquotes:

divide m n
m `divide` n

Los divisores de un número es una lista definida por comprensión:

divisores n = [d | d <- [1..n], d 'divide' n]

Esto es equivalente a utilizar la función filter:

divisores n = filter(divide n) [1..n]

El máximo común divisor puede definirse como:

mcd x y = maximum [d | d <- divisores x, d 'divide' y]

Otra forma de definir el mcd es utilizando composición de funciones:

mcd x y = máximum filter ('divide' y) . divisores $ x

donde f $ x = f x